- 残差

残差
普通残差
设线性回归模型为其中Y是由响应变量构成的n维向量,X是阶设计矩阵,β是p+1维向量,ε是n维随机变量。
回归系数的估计值



这解释了帽子矩阵与残差的关系,因为残差可以通过帽子矩阵与真实值得出。
内学生化残差
 残差(3)由差向量ε的的性质,得到。因此,对每个,有,其中是矩阵H对角线上的元素。
残差(3)由差向量ε的的性质,得到。因此,对每个,有,其中是矩阵H对角线上的元素。
用作为的估计值,称为标准化残差,或者称为内学生化残差。这因为的估计中用了包括第i个样本在内的全部数据。由可知,标准化残差近似服从标准正态分布。
外学生化残差
 残差(3)若记删除第i个样本数据后,由余下的n-1个样本数据求得的回归系数为,做的估计值,有,其中为设计矩阵X的第j行。称为学生化残差,或者称为外学生化残差。[1]
残差(3)若记删除第i个样本数据后,由余下的n-1个样本数据求得的回归系数为,做的估计值,有,其中为设计矩阵X的第j行。称为学生化残差,或者称为外学生化残差。[1]
特征
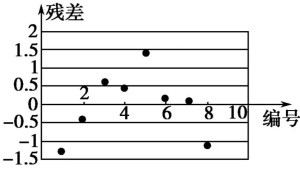
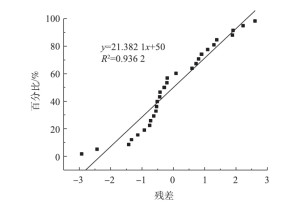 残差在回归分析中,测定值与按回归方程预测的值之差,以δ表示。残差δ遵从正态分布N(0,σ2)。(δ-残差的均值)/残差的标准差,称为标准化残差,以δ*表示。δ*遵从标准正态分布N(0,1)。实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点,不参与回归直线拟合。
残差在回归分析中,测定值与按回归方程预测的值之差,以δ表示。残差δ遵从正态分布N(0,σ2)。(δ-残差的均值)/残差的标准差,称为标准化残差,以δ*表示。δ*遵从标准正态分布N(0,1)。实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点,不参与回归直线拟合。
显然,有多少对数据,就有多少个残差。残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰。
分析
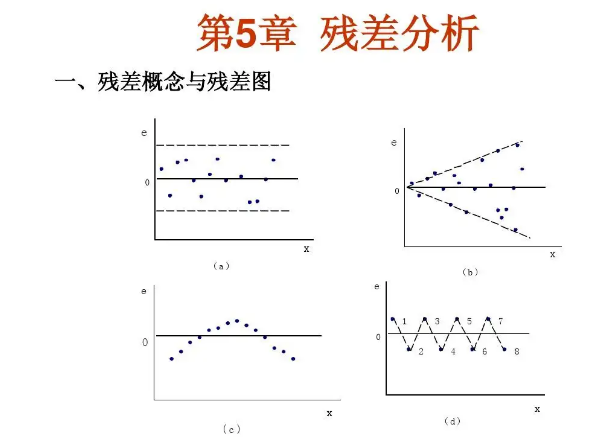
为了更深入地研究某一自变量与因变量的关系,人们还引进了偏残差。此外, 还有学生化残差、预测残差等。以某种残差为纵坐标,其它变量为横坐标作散点图,即残差图 ,它是残差分析的重要方法之一。通常横坐标的选择有三种:
(1)因变量的拟合值;
(2)自变量;
(3)当因变量的观测值为一时间序列时,横坐标可取观测时间或观测序号。
残差图的分布趋势可以帮助判明所拟合的线性模型是否满足有关假设。如残差是否近似正态分布、是否方差齐次,变量间是否有其它非线性关系及是否还有重要自变量未进入模型等。.当判明有某种假设条件欠缺时, 进一步的问题就是加以校正或补救。需分析具体情况,探索合适的校正方案,如非线性处理,引入新自变量,或考察误差是否有自相关性。



 求购
求购


