梯形中位线定理

梯形中位线定理是梯形的一个重要性质，在初中几何教学中占有重要地位。它既是对三角形中位线定理的拓展与应用，又为今后有关两条线平行和线段倍分关系的证明与应用提供了更为可行的方法。

梯形的中位线L平行于底边，且其长度为上底加下底和的一半，用符号表示是.

L=（a+b）/2

已知中位线长度和高，就能求出梯形的面积．

S梯=2Lh÷2=Lh

中位线在关于梯形的各种题型中都是一条得天独厚的辅助线。

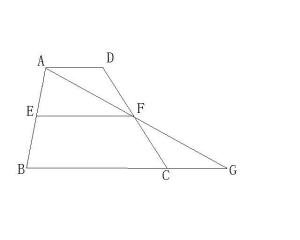梯形中位线定理证明如图，四边形ABCD是梯形，AD∥BC，E、F分别是AB、CD边上的中点，求证：EF∥AD，且EF=（AD+BC）/2

证明：

连接AF并延长交BC的延长线于G。

∵AD∥BC

∴∠ADF=∠GCF

∵F是CD的中点

∴DF=FC

∵∠AFD=∠CFG

∴△ADF≌△GCF(ASA)

∴AF=FG，AD=CG

∴F是AG的中点

∵E是AB的中点

∴EF是△ABG的中位线

∴EF∥BG,EF=BG/2=(BC+CG)/2

∴EF=(AD+BC)/2

∵AD∥BC

∴EF∥AD∥BC

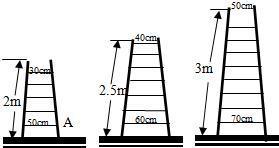如图的梯子。已知梯子每跨一步上升高度相同，则求内部横杆总长。

题示（做这些题目要注意题目的细节——上升高度相同，即每条横杆都是小梯形的中位线）。

如果同学没有掌握技巧，只会死算，那么大多只能做如图的最左的五步梯，可以设未知数解，时间消耗很大，尤其是运气不佳遇到中间或右边的多步梯，X、Y、Z的计算量非常大。

但是题目做多了，我总结了一个规律，以左图五步梯为例：五根横杆的总长为1/2（30cm+50cm）X5

中图七步梯为例：1/2(40cm+60cm)X7 那么同理，右图九步梯则是1/2(50cm+70cm)X9

总结一下就是1/2(上底+下底)Xn