- 二维正态分布

二维正态分布
中文名
二维正态分布
别称
二维高斯分布
应用学科
统计学
定律定义
满足下述的概率密度分布的随机变量分布叫做二维正态分布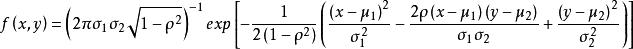
其中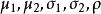 都是常数,我们称
都是常数,我们称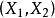 服从参数为
服从参数为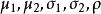 的二维正态分布,常把这个分布记作
的二维正态分布,常把这个分布记作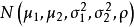 )。
)。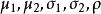 的范围分别为
的范围分别为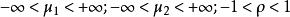
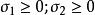 。这个函数在三维空间中的图像是一个椭圆切面的钟倒扣在
。这个函数在三维空间中的图像是一个椭圆切面的钟倒扣在![]() 平面上,其中心在(
平面上,其中心在(![]() )点。
)点。
公式验证
证明该函数是一个概率密度函数,其应该满足概率密度函数的基本性质:一是大于零,二是全空间上的积分等于1。第一点显而易见,下面给出条件二的证明。
做变换
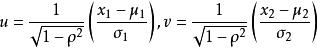
得
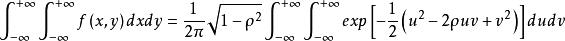
再做变量代换
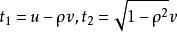
注意到
得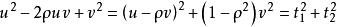
![]()
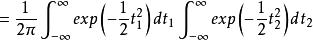
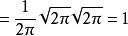
边缘概率密度
二维正态分布的两个边缘分布都是一维正态分布的形式:![]() 并且都不依赖于参数
并且都不依赖于参数![]() ,即
,即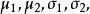 不同的
不同的![]() 对应不同的二维正态分布,但它们的边缘分布是一样的。这一事实表明,单由关于X和关于Y的边缘分布,不能确定随机变量X和Y的联合分布,但加入了结合紧密程度的参数
对应不同的二维正态分布,但它们的边缘分布是一样的。这一事实表明,单由关于X和关于Y的边缘分布,不能确定随机变量X和Y的联合分布,但加入了结合紧密程度的参数![]() ,就可以确定。
,就可以确定。
证明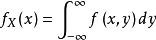 是一维正态分布
是一维正态分布
由于
于是
令
则有
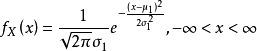
同理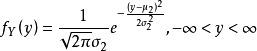
独立性
对于二维正态随机变量(X,Y),X和Y相互独立的充要条件是参数ρ=0。也即二维正态随机变量独立和不相关可以互推。以下给出证明过程。
必要性:如果ρ=0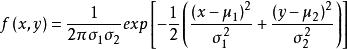
![]()
有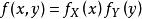
充分性:如果X和Y相互独立,由于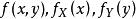 都是连续函数,有
都是连续函数,有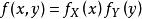 。
。
特别令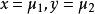 。得到
。得到
![]() 为使这一等式成立,从而ρ=0。[1]
为使这一等式成立,从而ρ=0。[1]
 收藏
收藏

相关百科
-
比亚迪宋Plus 联手博世/采用分布式驱动
2025-09-24 07:07:46 查看详情 -
比亚迪海洋系轿车最新谍照 联手博世/采用分布式驱动
2025-09-24 07:07:46 查看详情 -
比亚迪秦PLUS 联手博世/采用分布式驱动
2025-09-24 07:07:46 查看详情 -
比亚迪海豹正式开启预售 联手博世/采用分布式驱动
2025-09-24 07:07:46 查看详情 -
比亚迪秦PLUS内饰设计图曝光 联手博世/采用分布式驱动
2025-09-24 07:07:46 查看详情 -
nanosox空气分布系统
2025-09-24 07:07:46 查看详情 -
纤维织物空气分布系统
2025-09-24 07:07:46 查看详情


 求购
求购

