约翰逊噪声

该类型噪声是由约翰·约翰逊1926年在贝尔实验室发现并且第一次测量的。他向哈里·奈奎斯特描述了他的发现，奈奎斯特当时也在贝尔实验室并且能够解释这个结果。

约翰逊噪声与散粒噪声完全不同，散粒噪声包括额外的电流波动，当提供电压并伴随宏观电流开始流动时就会产生。一般情况下，上述定义适用于任何类型的导电介质的电荷载体（例如，电解质中的离子），而不只是电阻。可以通过一个能提供非理想电阻噪声的电压源串联一个无噪声的理想电阻来模拟。

单边功率谱密度，或电压变化（均方）带宽每赫兹，由下式给出：

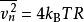
其中k_B是玻尔兹曼常数用焦耳每开尔文表示,T是电阻的绝对温度用开尔文表示，R是电阻值用欧姆(Ω)表示。

该公式可用于室温下的快速计算：

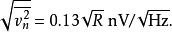例如，一个 1 kΩ 电阻温度在 300 K 时有

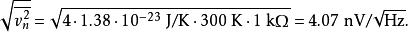对于给定带宽，电压给出

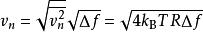
其中 Δf为已测噪声之上的带宽用赫兹表示。一个1 k 电阻器在室温及 10kHz带宽情况下的RMS噪声电压是400 nV。一个有用的经验法则需要记住的是，50 Ω 在室温及 1 Hz 带宽下对应于 1 nV 的噪声。

电阻器短路连接时的耗散噪声功率

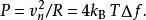
电阻器所产生的噪声可以传递至其余电路；最大的噪声功率传递发生在噪声产生阻抗与剩余电路的戴维南等效阻抗阻抗匹配时。在这种情况下两部分阻抗中的任意一个的耗散噪声均作用在其本身和其他电阻。由于其中的任何一个电阻只有一半的压降，因此噪声功率

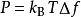此处P是约翰逊噪声功率用瓦表示。注意这是独立的噪声产生阻抗。

噪声源也可以通过电流源并联电阻方式来模拟，通过诺顿等效相应的只要简单地除以R便可以得到。这里给出该电流源的均方根值为：

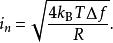约翰逊噪声是所有电阻的固有属性，并不是糟糕的设计或制造商的标记，尽管电阻可能还含有多余的噪声。

电容器上的约翰逊噪声被称为kTC噪声。约翰逊噪声在一个RC电路有一个非常简单的表达，当作阻抗（R）从公式中移除。这是因为更高的R有助于更好的滤波但也产生更多噪声。RC 电路的噪声带宽是 1/(4RC)，它可代入上述公式，以消除R。这样一个滤波器产生的噪声电压的均方与 RMS 为：

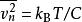
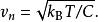
约翰逊噪声在电阻中占100%的kTC的噪声。

在极端的情况下开启一个理想开关会存留“重置噪声”在电容器上，阻抗是无限的，但公式仍然适用；但是，现在 RMS 必须解释为非时间上的平均，但是许多这样的重复事件的平均，由于电压在带宽为零时为常数。从这个意义上讲，RC电路的约翰逊噪声可以看作是固有的、电子在电容器上数量分布热力学效应，甚至不涉及电阻。

噪声并非电容器本身引起的，而是由电容器上的一定数量电荷的热力学波动引起的。一旦电容器与导体电路断开连接、热力学波动便“冻结”在如上面给出的一个标准偏差的随机值上。

电容的复位噪声传感器通常是一个有限噪声源，例如在图象传感器中。 作为电压噪声的一种替代，电容的复位噪声也可以进行定量为电荷的标准偏差，有

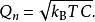
由于电荷差异是，噪声常被称为“KTC 噪声”。

任何系统在热平衡有状态变量与平均能量的kT/2 每自由度。使用电容能量(E=½CV)，意味着电容器上的噪声能量在一个容器中可以看出也为½C(kT/C)，或kT/2. 电容器上的约翰逊噪声可以从该关系导出，无需考虑阻抗。