点斜式

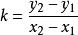在平面直角坐标系中，如果直线L经过点A和B，其中x1≠x2，那么是L的一个方向向量，于是直线L的斜率，再由k=tanα（0≤α<π），可求出直线L的倾斜角α.记tanα=k，方程叫做直线的点斜式方程，其中是直线上一点。

直线方程一般有以下八种描述方式：点斜式、截距式、两点式、一般式、斜截式、法线式、点向式、法向式。其中点斜式适用于k≠0，直线不垂直于x轴的情况。

点斜式方程普遍用于导数当中，用已知切线上一点和曲线方程的导数（方程上某点切线的斜率）求切线方程时用。适用于知道一个点的坐标和直线斜率，求直线方程的题目。

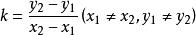
当直线与x轴垂直时，k不存在时，直线可表示为

当直线与y轴垂直时，k=0时，直线可表示为

局限性：当α为即直线与x轴垂直时，tanα无意义，不存在点斜式方程。

若直线经过点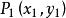，且斜率为k，求L1方程。

设点P(x，y)是直线上不同于点P1的任意一点，直线的斜率应等与直线的斜率，根据经过两点的直线的斜率公式得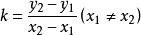

所以，直线：

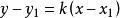
说明：

(1)这个方程是由直线上一点和斜率确定的，这一点必须在直线上，否则点斜式方程不成立；

(2)当直线的倾斜角为0°时，直线方程为；

(3)当直线倾斜角为90°时，直线没有斜率，它的方程不能用点斜式表示，这时直线方程为。^[2]

开始学习时通常是求两条斜率不相等（非平行）的直线的交点，接着是与抛物线的交点，通过点斜式方程代入抛物线方程，求出交点的个数和坐标。还有平面解析几何，比如椭圆、圆、双曲线、抛物线等圆锥曲线问题解决的固定套路，方程联立的时候就习惯用点斜式。

在求曲线切线方程中，一般会告诉切点和曲线方程。这时利用导数公式可求出切线斜率k，利用点斜式可以表示此直线方程。

另外，有时题目会告诉曲线外一点(a,b)和曲线方程，这时只需设切点坐标A(x,y)，利用导数公式求出导数的表达式M，再使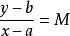即可求出切点A的坐标。利用点斜式可将方程表示出来。^[2]