反正切函数

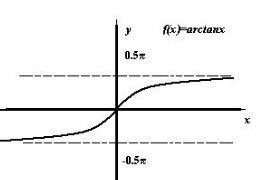反正切函数  函数y=tanx,（x∈（-π/2,π/2））的 反函数，记作y=arctanx，叫做反正切函数，其定义域为R。反正切函数是 反三角函数的一种。

同样，由于 正切函数y=tanx在定义域R上不具有一一对应的关系，所以不存在反函数。

注意这里选取是正切函数的一个 单调区间。

反正切函数  定义域：R

值 域：(-π/2,π/2)

单调性： 增函数

奇偶性：奇函数

周期性：不是 周期函数

单调性：（－∞，﹢∞）单调递增

tan(arctana)=a

arctan(-x)=-arctanx

arctan A + arctan B

=arctan[(A+B)/(1-AB)]

arctan A - arctan B

=arctan[(A-B)/(1+AB)]

反三角函数在无穷小替换公式中的应用：

当x→0时，arctanx~x

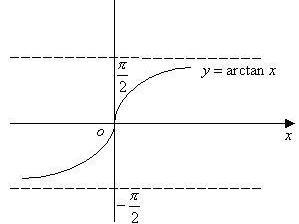反正切函数  反正切函数的大致图像如图所示，显然与函数y=tanx,（x∈R）关于直线y=x对称，且渐近线为y=π/2和y=-π/2