差异量数

差异量数大，表示各数值分布的范围广且参差不齐；差异量数小，表示各数值较集中、整齐，波动的范围幅度小。因此，集中量数的代表性如何，可由差异量数反映。差异量数愈大，则集中量数的代表性愈小；差异量数愈小，则集中量数的代表性愈大。所以，考察某种分布的差异量数，有助于对集中量数的理解。^[1]

常见的差异量数有平均差、方差、标准差、全距、四分差、百分差等。

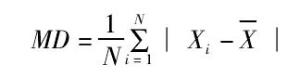图1 平均数公式一组数据(样本)Xi，i = 1，…，N(1)的平均差公式为图1

它是算术平均数与各数据距离的平均，有效地利用了信息，能直接很好地反映这组数据的差异程度。但由于MD（平均数）用了绝对值，难以进行代数运算，理论分析困难，所以运用较少。

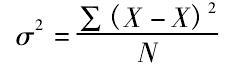图2方差的公式为图2

它是将MD中的距离改为距离的平方得到。方差可有效地利用信息，且能很好地反映这组数据的差异程度。这样改变后，虽然不如平均差反映差异那么直接，但避免了绝对值，从而进行数学处理更加方便，应用最广。

全距是用来表示统计资料中的变异量数(measures of variation)，是最大值与最小值之间的差距，即最大值减最小值后所得之数据。其适用于等距变量、比率变量，不适用于名义变量或次序变量。

全距也称为极差，是指总体各单位的两个极端标志值之差，即：R=最大标志值－最小标志值。

因此，全距（R）可反映总体标志值的差异范围。

百分差与四分差只利用了数据的部分信息，不能进行代数运算，反应不灵敏，但当两极端数据不清楚或数据信息不全时，只能用百分差与四分差。

百分差计算公式：

图3

四分差计算公式:

图4

全距、百分差与四分差都只利用了数据的部分信息，一般是在数据信息不全，平均差和方差及其改进量不能用时选用。

标准差（Standard Deviation），概率统计中最常使用，衡量统计分布程度（statistical dispersion）的量数。标准差的定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根，反映组内个体间的离散程度。

标准计算公式：

图5

几种差异量数的比较见图6

图6 几种差异量数的比较