- 贝祖定理

贝祖定理
中文名称
贝祖定理
别称
裴蜀定理
应用学科
初等数论
定理定义
 合并图册(2)
合并图册(2)
定义整数a,b的一个线性组合是指形如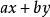 的整数,其中x,y是整数。那么贝祖定理是说对整数a,b(如果我们定义
的整数,其中x,y是整数。那么贝祖定理是说对整数a,b(如果我们定义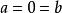 时,
时,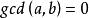 ),
),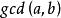 是a,b的一个线性组合(其中
是a,b的一个线性组合(其中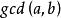 是a,b的最大公因数,简记为
是a,b的最大公因数,简记为![]() )。
)。
验证推导
若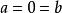 ,则
,则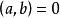 .结论显然.
.结论显然.
不妨设![]() .考虑由
.考虑由![]() 所有的线性组合组成的集合
所有的线性组合组成的集合![]()
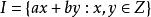
分别取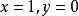 和
和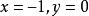 :
:![]() .由于正实数集对所有实数有三分法成立,故
.由于正实数集对所有实数有三分法成立,故![]() 中必定有一个为正(已令
中必定有一个为正(已令![]() ).设
).设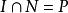 ,则
,则![]() .
.
由最小数原理知,![]() 中有最小正整数,不妨设为
中有最小正整数,不妨设为![]() .
.
因为![]() ,所以
,所以![]() 是
是![]() 的一个线性组合:
的一个线性组合:![]()
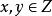 ,
,
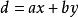 由带余除法可知:
由带余除法可知: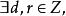 使得
使得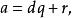 其中
其中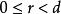 .假设
.假设![]() ,则:
,则:
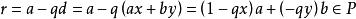 这与
这与![]() 是
是![]() 的最小元矛盾.故
的最小元矛盾.故![]() ,即
,即![]() 是
是![]() 的因子.类似地,可证
的因子.类似地,可证![]() 是
是![]() 的因子.故
的因子.故![]() 是
是![]() 和
和![]() 的公因子.
的公因子.
若![]() 是
是![]() 和
和![]() 的任意一个公因子,则设
的任意一个公因子,则设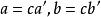 .因为
.因为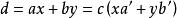 ,所以
,所以![]() 整除
整除![]() ,所以
,所以![]() .故
.故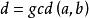 .
.
应用例子
- 若a |bc,且(a,b)=1,则a |c证明:∵(a,b)=1,由贝祖定理,存在x,y∈Z,使得 ax+by=1∴ (ax+by)c = c∴acx+bcy = c∵ a | ac,a | bc∴ a | acx+bcy∴a | c命题得证
2.若a |c,b |c,且(a,b)=1,则ab |c
3.设m为正整数,则(ma,mb)=m(a,b),[ma,mb]=m[a,b]
4.设a,b都为正整数,则(a,b)·[a,b]=ab[1]

相关百科
-
雷诺拉古那古贝性能如何及其简介
2025-09-25 22:18:35 查看详情


 求购
求购








