哈夫曼编码

1951年，哈夫曼和他在MIT信息论的同学需要选择是完成学期报告还是期末考试。导师Robert M. Fano给他们的学期报告的题目是，寻找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的。由于这个算法，学生终于青出于蓝，超过了他那曾经和信息论创立者香农共同研究过类似编码的导师。哈夫曼使用自底向上的方法构建二叉树，避免了次优算法Shannon-Fano编码的最大弊端──自顶向下构建树。

1952年，David A. Huffman在麻省理工攻读博士时发表了《一种构建极小多余编码的方法》（A Method for the Construction of Minimum-Redundancy Codes）一文，它一般就叫做Huffman编码。

Huffman在1952年根据香农（Shannon）在1948年和范若（Fano）在1949年阐述的这种编码思想提出了一种不定长编码的方法，也称霍夫曼（Huffman）编码。霍夫曼编码的基本方法是先对图像数据扫描一遍，计算出各种像素出现的概率，按概率的大小指定不同长度的唯一码字，由此得到一张该图像的霍夫曼码表。编码后的图像数据记录的是每个像素的码字，而码字与实际像素值的对应关系记录在码表中。

赫夫曼编码是可变字长编码(VLC)的一种。 Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长 度最短的码字，有时称之为最佳编码，一般就称Huffman编码。下面引证一个定理，该定理保证了按字符出现概率分配码长，可使平均码长最短。

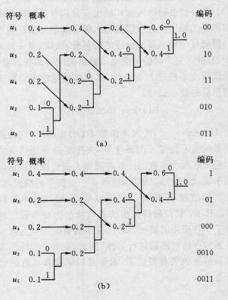图1 赫夫曼编码原理设某信源产生有五种符号u1、u2、u3、u4和u5，对应概率P1=0.4，P2=0.1，P3=P4=0.2，P5=0.1。首先，将符号按照概率由大到小排队，如图所示。编码时，从最小概率的两个符号开始，可选其中一个支路为0，另一支路为1。这里，我们选上支路为0，下支路为1。再将已编码的两支路的概率合并，并重新排队。多次重复使用上述方法直至合并概率归一时为止。从图（a）和（b）可以看出，两者虽平均码长相等，但同一符号可以有不同的码长，即编码方法并不唯一，其原因是两支路概率合并后重新排队时，可能出现几个支路概率相等，造成排队方法不唯一。一般，若将新合并后的支路排到等概率的最上支路，将有利于缩短码长方差，且编出的码更接近于等长码。这里图（a）的编码比（b）好。

赫夫曼码的码字（各符号的代码）是异前置码字，即任一码字不会是另一码字的前面部分，这使各码字可以连在一起传送，中间不需另加隔离符号，只要传送时不出错，收端仍可分离各个码字，不致混淆。

实际应用中，除采用定时清洗以消除误差扩散和采用缓冲存储以解决速率匹配以外，主要问题是解决小符号集合的统计匹配，例如黑（1）、白（0）传真信源的统计匹配，采用0和1不同长度游程组成扩大的符号集合信源。游程，指相同码元的长度（如二进码中连续的一串0或一串1的长度或个数）。按照CCITT标准，需要统计2×1728种游程（长度），这样，实现时的存储量太大。事实上长游程的概率很小，故CCITT还规定：若l表示游程长度，则l=64q+r。其中q称主码，r为基码。编码时，不小于64的游程长度由主码和基码组成。而当l为64的整数倍时，只用主码的代码，已不存在基码的代码。

长游程的主码和基码均用赫夫曼规则进行编码，这称为修正赫夫曼码，其结果有表可查。该方法已广泛应用于文件传真机中。

哈夫曼编码在变字长编码中，如果码字长度严格按照对应符号出现的概率大小逆序排列，则其平 均码字长度为最小。

现在通过一个实例来说明上述定理的实现过程。设将信源符号按出现的概率大小顺序排列为 ：

U： ( a1 a2 a3 a4 a5 a6 a7 ) [1]

0.20 0.19 0.18 0.17 0.15 0.10 0.01

给概率最小的两个符号a6与a7分别指定为“1”与“0”，然后将它们的概率相加再与原来的 a1~a5组合并重新排序成新的原为：

U′： ( a1 a2 a3 a4 a5 a6′ )

0.20 0.19 0.18 0.17 0.15 0.11

对a5与a′6分别指定“1”与“0”后，再作概率相加并重新按概率排序得

U″：（0.26 0.20 0.19 0.18 0.17）…

直到最后得 U″″：（0.61 0.39）

赫夫曼编码的具体方法：先按出现的概率大小排队，把两个最小的概率相加，作为新的概率 和剩余的概率重新排队，再把最小的两个概率相加，再重新排队，直到最后变成1。每次相 加时都将“0”和“1”赋与相加的两个概率，读出时由该符号开始一直走到最后的“1”， 将路线上所遇到的“0”和“1”按最低位到最高位的顺序排好，就是该符号的赫夫曼编码。

例如a7从左至右，由U至U″″，其码字为1000；

a6按路线将所遇到的“0”和“1”按最低位到最高位的顺序排好，其码字为1001…

用赫夫曼编码所得的平均比特率为：Σ码长×出现概率

上例为：0.2×2+0.19×2+0.18×3+0.17×3+0.15×3+0.1×4+0.01×4=2.72 bit

可以算出本例的信源熵为2.61bit，二者已经是很接近了。

哈夫曼编码是上个世纪五十年代由哈夫曼教授研制开发的,它借助了数据结构当中的树型结构,在哈夫曼算法的支持下构造出一棵最优二叉树,我们把这类树命名为哈夫曼树.因此,准确地说,哈夫曼编码是在哈夫曼树的基础之上构造出来的一种编码形式,它的本身有着非常广泛的应用.那么,哈夫曼编码是如何来实现数据的压缩和解压缩的呢?

众所周知,在计算机当中,数据的存储和加工都是以字节作为基本单位的,一个西文字符要通过一个字节来表达,而一个汉字就要用两个字节,我们把这种每一个字符都通过相同的字节数来表达的编码形式称为定长编码.以西文为例,例如我们要在计算机当中存储这样的一句话:I am a teacher.就需要15个字节,也就是120个二进制位的数据来实现.与这种定长编码不同的是,哈夫曼编码是一种变长编码.它根据字符出现的概率来构造平均长度最短的编码.换句话说如果一个字符在一段文档当中出现的次数多,它的编码就相应的短,如果一个字符在一段文档当中出现的次数少,它的编码就相应的长.当编码中,各码字的长度严格按照对应符号出现的概率大小进行逆序排列时,则编码的平均长度是最小的.这就是哈夫曼编码实现数据压缩的基本原理.要想得到一段数据的哈夫曼编码,需要用到三个步骤:第一步:扫描需编码的数据,统计原数据中各字符出现的概率.第二步:利用得到的概率值创建哈夫曼树.第三步:对哈夫曼树进行编码,并把编码后得到的码字存储起来.

因为定长编码已经用相同的位数这个条件保证了任一个字符的编码都不会成为其它编码的前缀,所以这种情况只会出现在变长编码当中,要想避免这种情况,我们就必须用一个条件来制约定长编码,这个条件就是要想成为压缩编码,变长编码就必须是前缀编码.什么是前缀编码呢?所谓的前缀编码就是任何一个字符的编码都不能是另一个字符编码的前缀.

那么哈夫曼编码是否是前缀编码呢?观察a、b、c、d构成的编码树,可以发现b之所以成为c的前缀,是因为在这棵树上,b成为了c的父结点,从在哈夫曼树当中,原文档中的数据字符全都分布在这棵哈夫曼树的叶子位置,从而保证了哈夫曼编码当中的任何一个字符的编码都不能是另一个字符编码的前缀.也就是说哈夫曼编码是一种前缀编码,也就保证了解压缩过程当中译码的准确性.哈夫曼编码的解压缩过程也相对简单,就是将编码严格按照哈夫曼树进行翻译就可以了,例如遇到000,就可以顺着哈夫曼树找到I,遇到101就可以顺着哈夫曼树找到空格,以此类推,我们就可以很顺利的找到原来所有的字符.哈夫曼编码是一种一致性编码,有着非常广泛的应用,例如在JPEG文件中,就应用了哈夫曼编码来实现最后一步的压缩;在数字电视大力发展的今天,哈夫曼编码成为了视频信号的主要压缩方式.应当说,哈夫曼编码出现,结束了熵编码不能实现最短编码的历史,也使哈夫曼编码成为一种非常重要的无损编码.

静态哈夫曼方法的最大缺点就是它需要对原始数据进行两遍扫描:第一遍统计原始数据中各字符出现的频率,利用得到的频率值创建哈夫曼树并将树的有关信息保存起来,便于解压时使用;第二遍则根据前面得到的哈夫曼树对原始数据进行编码,并将编码信息存储起来。这样如果用于网络通信中,将会引起较大的延时;对于文件压缩这样的应用场合,额外的磁盘访间将会降低该算法的数据压缩速度。

Faller等人提出了动态哈夫曼编码方法,它对数据编码的依据是动态变化的哈夫曼树,也就是说,对第t+1个字符编码是根据原始数据中前t个字符得到的哈夫曼树来进行的.压缩和解压子程序具有相同的初始化树,每处理完一个字符,压缩和解压方使用相同的算法修改哈夫曼树,因而该方法不需要为解压而保存树的有关信息。压缩和解压一个字符所需的时间与该字符的编码长度成正比,因而该过程可以实时进行。

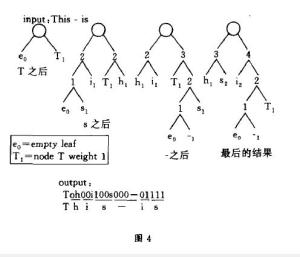
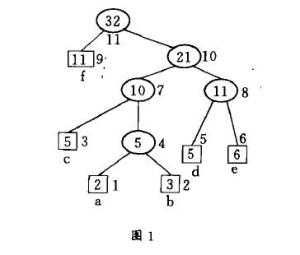
我们分两步来进行。第一步我们把前t个字符的哈夫曼树转换成它的另一种形式,在该树中只需在第二步中简单地把由根到叶结点alol路径上的所有结点重量加1,就可以变成前t+1个字符的哈夫曼树。其过程就是以叶结点a(it+1)为初始的当前结点,重复地将当前结点与具有同样重量的序号最大的结点进行交换,并使得后者的父结点成为新的当前结点,直到遇到根结点为止。以图1为例,结点2无需进行交换,因而结点4成为新的当前结点,结点4与结点5

交换,结点8就成为当前结点,最后结点8与结点9进行交换,结点n成为当前结点,结束该循环。到此为止,第一步已经完成,其结果如图2所示,容易验证它也是前t个字符的一种哈夫曼树形式,因为交换只是在同重量结点之间进行。第二步通过将根到叶结点a(it+1)路径上的所有结点重量加1,该树就变成了前t+1个字符的哈夫曼树。如图3所示。一个比较完整的动态哈夫曼编码实例如图4所示。

哈弗曼编码在信息论中应用举例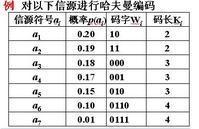哈弗曼编码在信息论中应用举例哈夫曼树─即最优二叉树，带权路径长度最小的二叉树，经常应用于数据压缩。 在计算机信息处理中，“哈夫曼编码”是一种一致性编码法（又称“熵编码法”），用于数据的无损耗压缩。这一术语是指使用一张特殊的编码表将源字符（例如某文件中的一个符号）进行编码。这张编码表的特殊之处在于，它是根据每一个源字符出现的估算概率而建立起来的（出现概率高的字符使用较短的编码，反之出现概率低的则使用较长的编码，这便使编码之后的字符串的平均期望长度降低，从而达到无损压缩数据的目的）。这种方法是由David.A.Huffman发展起来的。 例如，在英文中，e的出现概率很高，而z的出现概率则最低。当利用哈夫曼编码对一篇英文进行压缩时，e极有可能用一个位(bit)来表示，而z则可能花去25个位（不是26）。用普通的表示方法时，每个英文字母均占用一个字节（byte），即8个位。二者相比，e使用了一般编码的1/8的长度，z则使用了3倍多。若能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。

为了让它(huffman.cpp)快速运行，同时不使用任何动态库，比如STL或者MFC。它压缩1M数据少于100ms（P3处理器，主频1G）。

压缩代码非常简单，首先用ASCII值初始化511个哈夫曼节点：

CHuffmanNode nodes[511];

for(int nCount = 0; nCount < 256; nCount++)

nodes[nCount].byAscii = nCount;

其次，计算在输入缓冲区数据中，每个ASCII码出现的频率：

for(nCount = 0; nCount < nSrcLen; nCount++)

nodes[pSrc[nCount]].nFrequency++;

然后，根据频率进行排序：

qsort(nodes, 256, sizeof(CHuffmanNode), frequencyCompare);

哈夫曼树，获取每个ASCII码对应的位序列：

int nNodeCount = GetHuffmanTree(nodes);

构造哈夫曼树非常简单，将所有的节点放到一个队列中，用一个节点替换两个频率最低的节点，新节点的频率就是这两个节点的频率之和。这样，新节点就是两个被替换节点的父节点了。如此循环，直到队列中只剩一个节点（树根）。

// parent node

pNode = &nodes[nParentNode++];

// pop first child

pNode->pLeft = PopNode(pNodes, nBackNode--, false);

// pop second child

pNode->pRight = PopNode(pNodes, nBackNode--, true);

// adjust parent of the two poped nodes

pNode->pLeft->pParent = pNode->pRight->pParent = pNode;

// adjust parent frequency

pNode->nFrequency = pNode->pLeft->nFrequency + pNode->pRight->nFrequency;

有一个好的诀窍来避免使用任何队列组件。ASCII码只有256个，但实际分配了511个(CHuffmanNode nodes[511])，前255个记录ASCII码，而用后255个记录哈夫曼树中的父节点。并且在构造树的时候只使用一个指针数组(ChuffmanNode *pNodes[256])来指向这些节点。同样使用两个变量来操作队列索引(int nParentNode = nNodeCount;nBackNode = nNodeCount –1)。

接着，压缩的最后一步是将每个ASCII编码写入输出缓冲区中：

int nDesIndex = 0;

// loop to write codes

for(nCount = 0; nCount < nSrcLen; nCount++)

{

*(DWORD*)(pDesPtr+(nDesIndex>>3)) |=

nodes[pSrc[nCount]].dwCode << (nDesIndex&7);

nDesIndex += nodes[pSrc[nCount]].nCodeLength;

}

(nDesIndex>>3): >>3 以8位为界限右移后到达右边字节的前面

(nDesIndex&7): &7 得到最高位.

此外，在压缩缓冲区中，必须保存哈夫曼树的节点以及位序列，这样才能在解压缩时重新构造哈夫曼树（只需保存ASCII值和对应的位序列）。

解压缩比构造哈夫曼树要简单的多，将输入缓冲区中的每个编码用对应的ASCII码逐个替换就可以了。只要记住，这里的输入缓冲区是一个包含每个ASCII值的编码的位流。因此，为了用ASCII值替换编码，我们必须用位流搜索哈夫曼树，直到发现一个叶节点，然后将它的ASCII值添加到输出缓冲区中：

int nDesIndex = 0;

DWORD nCode;

while(nDesIndex < nDesLen)

{

nCode = (*(DWORD*)(pSrc+(nSrcIndex>>3)))>>(nSrcIndex&7);

pNode = pRoot;

while(pNode->pLeft)

{

pNode = (nCode&1) ? pNode->pRight : pNode->pLeft;

nCode >>= 1;

nSrcIndex++;

}

pDes[nDesIndex++] = pNode->byAscii;

}

#include <stdio.h>

#include <stdlib.h>

#include <string.h>

#include <math.h>

#define M 100

typedef struct Fano_Node

{

char ch;

float weight;

}FanoNode[M];

typedef struct node

{

int start;

int end;

struct node *next;

}LinkQueueNode;

typedef struct

{

LinkQueueNode *front;

LinkQueueNode *rear;

}LinkQueue;

//建立队列

void EnterQueue(LinkQueue *q,int s,int e)

{

LinkQueueNode *NewNode;

//生成新节点

NewNode=(LinkQueueNode*)malloc(sizeof( LinkQueueNode ));

if(NewNode!=NULL)

{

NewNode->start=s;

NewNode->end=e;

NewNode->next=NULL;

q->rear->next=NewNode;

q->rear=NewNode;

}

else

{

printf("Error!");

exit(-1);

}

}

//按权分组

void Divide(FanoNode f,int s,int *m,int e)

{

int i;

float sum,sum1;

sum=0;

for(i=s;i<=e;i++)

sum+=f[i].weight;//

*m=s;

sum1=0;

for(i=s;i<e;i++)

{

sum1+=f[i].weight;

*m=fabs(sum-2*sum1)>fabs(sum-2*sum1-2*f[i+1].weight)?(i+1):*m;

if(*m==i) break;

}

}

void main()

{

int i,j,n,max,m,h[M];

int sta,end;

float w;

char c,fc[M][M];

FanoNode FN;

LinkQueueNode *p;

LinkQueue *Q;

//初始化队Q

Q=(LinkQueue *)malloc(sizeof(LinkQueue));

Q->front=(LinkQueueNode*)malloc(sizeof(LinkQueueNode));

Q->rear=Q->front;

Q->front->next=NULL;

printf("\t***FanoCoding***\n");

printf("Please input the number of node:");

//输入信息

scanf("%d",&n);

//超过定义M,退出

if(n>=M)

{

printf(">=%d",M);

exit(-1);

}

i=1; //从第二个元素开始录入

while(i<=n)

{

printf("%d weight and node:",i);

scanf("%f %c",&FN[i].weight,&FN[i].ch);

for(j=1;j<i;j++)

{

if(FN[i].ch==FN[j].ch)//查找重复

{

printf("Same node!!!\n"); break;

}

}

if(i==j)

i++;

}

//排序(降序)

for(i=1;i<=n;i++)

{

max=i+1;

for(j=max;j<=n;j++)

max=FN[max].weight<FN[j].weight?j:max;

if(FN[i].weight<FN[max].weight)

{

w=FN[i].weight;

FN[i].weight=FN[max].weight;

FN[max].weight=w;

c=FN[i].ch;

FN[i].ch=FN[max].ch;

FN[max].ch=c;

}

}

for(i=1;i<=n;i++) //初始化h

h[i]=0;

EnterQueue(Q,1,n); //1和n进队

while(Q->front->next!=NULL)

{

p=Q->front->next; //出队

Q->front->next=p->next;

if(p==Q->rear)

Q->rear=Q->front;

sta=p->start;

end=p->end;

free(p);

Divide(FN,sta,&m,end); /*按权分组*/

for(i=sta;i<=m;i++)

{

fc[i][h[i]]='0';

++h[i];

}

if(sta!=m)

EnterQueue(Q,sta,m);

else

fc[sta][h[sta]]='\0';

for(i=m+1;i<=end;i++)

{

fc[i][h[i]]='1';

++h[i];

}

if(m==sta&&(m+1)==end)

//如果分组后首元素的下标与中间元素的相等，

//并且和最后元素的下标相差为1，则编码码字字符串结束

{

fc[m][h[m]]='\0';

fc[end][h[end]]='\0';

}

else

EnterQueue(Q,m+1,end);

}

for(i=1;i<=n;i++) /*打印编码信息*/

{

printf("%c:",FN[i].ch);

printf("%s\n",fc[i]);

}

system("pause");

}^[2]

#include <stdio.h>

#include <stdlib.h>

#include <string.h>

#define N 100

#define M 2*N-1

typedef char * HuffmanCode[2*M];//haffman编码

typedef struct

{

int weight;//权值

int parent;//父节节点

int LChild;//左子节点

int RChild;//右子节点

}HTNode,Huffman[M+1];//huffman树

typedef struct Node

{

int weight; //叶子结点的权值

char c; //叶子结点

int num; //叶子结点的二进制码的长度

}WNode,WeightNode[N];

/***产生叶子结点的字符和权值***/

void CreateWeight(char ch[],int *s,WeightNode CW,int *p)

{

int i,j,k;

int tag;

*p=0;//叶子节点个数

//统计字符出现个数,放入CW

for(i=0;ch[i]!='\0';i++)

{

tag=1;

for(j=0;j<i;j++)

if(ch[j]==ch[i])

{

tag=0;

break;

}

if(tag)

{

CW[++*p].c=ch[i];

CW[*p].weight=1;

for(k=i+1;ch[k]!='\0';k++)

if(ch[i]==ch[k])

CW[*p].weight++;//权值累加

}

}

*s=i;//字符串长度

}

/********创建HuffmanTree********/

void CreateHuffmanTree(Huffman ht,WeightNode w,int n)

{

int i,j;

int s1,s2;

//初始化哈夫曼树

for(i=1;i<=n;i++)

{

ht[i].weight =w[i].weight;

ht[i].parent=0;

ht[i].LChild=0;

ht[i].RChild=0;

}

for(i=n+1;i<=2*n-1;i++)

{

ht[i].weight=0;

ht[i].parent=0;

ht[i].LChild=0;

ht[i].RChild=0;

}

for(i=n+1;i<=2*n-1;i++)

{

for(j=1;j<=i-1;j++)

if(!ht[j].parent)

break;

s1=j; //找到第一个双亲为零的结点

for(;j<=i-1;j++)

if(!ht[j].parent)

s1=ht[s1].weight>ht[j].weight?j:s1;

ht[s1].parent=i;

ht[i].LChild=s1;

for(j=1;j<=i-1;j++)

if(!ht[j].parent)

break;

s2=j; //找到第二个双亲为零的结点

for(;j<=i-1;j++)

if(!ht[j].parent)

s2=ht[s2].weight>ht[j].weight?j:s2;

ht[s2].parent=i;

ht[i].RChild=s2;

ht[i].weight=ht[s1].weight+ht[s2].weight;//权值累加

}

}

/***********叶子结点的编码***********/

void CrtHuffmanNodeCode(Huffman ht,char ch[],HuffmanCode h,WeightNode weight,int m,int n)

{

int i,c,p,start;

char *cd;

cd=(char *)malloc(n*sizeof(char));

cd[n-1]='\0';//末尾置0

for(i=1;i<=n;i++)

{

start=n-1; //cd串每次从末尾开始

c=i;

p=ht[i].parent;//p在n+1至2n-1

while(p) //沿父亲方向遍历,直到为0

{

start--;//依次向前置值

if(ht[p].LChild==c)//与左子相同,置0

cd[start]='0';

else //否则置1

cd[start]='1';

c=p;

p=ht[p].parent;

}

weight[i].num=n-start; //二进制码的长度(包含末尾0)

h[i]=(char *)malloc((n-start)*sizeof(char));

strcpy(h[i],&cd[start]);//将二进制字符串拷贝到指针数组h中

}

free(cd);//释放cd内存

system("pause");

}

/*********所有字符的编码*********/

void CrtHuffmanCode(char ch[],HuffmanCode h,HuffmanCode hc,WeightNode weight,int n,int m)

{

int i,k;

for(i=0;i<m;i++)

{

for(k=1;k<=n;k++) /*从weight[k].c中查找与ch[i]相等的下标K*/

if(ch[i]==weight[k].c)

break;

hc[i]=(char *)malloc((weight[k].num)*sizeof(char));

strcpy(hc[i],h[k]); //拷贝二进制编码

}

}

/*****解码*****/

void TrsHuffmanTree(Huffman ht,WeightNode w,HuffmanCode hc,int n,int m)

{

int i=0,j,p;

printf("***StringInformation***\n");

while(i<m)

{

p=2*n-1;//从父亲节点向下遍历直到叶子节点

for(j=0;hc[i][j]!='\0';j++)

{

if(hc[i][j]=='0')

p=ht[p].LChild;

else

p=ht[p].RChild;

}

printf("%c",w[p].c); /*打印原信息*/

i++;

}

}

/*****释放huffman编码内存*****/

void FreeHuffmanCode(HuffmanCode h,HuffmanCode hc,int n,int m)

{

int i;

for(i=1;i<=n;i++)//释放叶子结点的编码

free(h[i]);

for(i=0;i<m;i++) //释放所有结点的编码

free(hc[i]);

}

void main()

{

int i,n=0; /*n为叶子结点的个数*/

int m=0; /*m为字符串ch[]的长度*/

char ch[N]; /*ch[N]存放输入的字符串*/

Huffman ht; /*Huffman二叉数*/

HuffmanCode h,hc; /*h存放叶子结点的编码，hc 存放所有结点的编码*/

WeightNode weight; /*存放叶子结点的信息*/

printf("\t***HuffmanCoding***\n");

printf("please input information :");

gets(ch); /*输入字符串*/

CreateWeight(ch,&m,weight,&n); /*产生叶子结点信息，m为字符串ch[]的长度*/

printf("***WeightInformation***\n Node ");

for(i=1;i<=n;i++) /*输出叶子结点的字符与权值*/

printf("%c ",weight[i].c);

printf("\nWeight ");

for(i=1;i<=n;i++)

printf("%d ",weight[i].weight);

CreateHuffmanTree(ht,weight,n); /*产生Huffman树*/

printf("\n***HuffamnTreeInformation***\n");

printf("\ti\tweight\tparent\tLChild\tRChild\n");

for(i=1;i<=2*n-1;i++) /*打印Huffman树的信息*/

printf("\t%d\t%d\t%d\t%d\t%d\n",i,ht[i].weight,ht[i].parent,ht[i].LChild,ht[i].RChild);

CrtHuffmanNodeCode(ht,ch,h,weight,m,n); /*叶子结点的编码*/

printf(" ***NodeCode***\n"); /*打印叶子结点的编码*/

for(i=1;i<=n;i++)

{

printf("\t%c:",weight[i].c);

printf("%s\n",h[i]);

}

CrtHuffmanCode(ch,h,hc,weight,n,m); /*所有字符的编码*/

printf("***StringCode***\n"); /*打印字符串的编码*/

for(i=0;i<m;i++)

printf("%s",hc[i]);

system("pause");

TrsHuffmanTree(ht,weight,hc,n,m); /*解码*/

FreeHuffmanCode(h,hc,n,m);

system("pause");

}^[3]

Matlab 中简易实现Huffman编译码：

n=input('Please input the total number: ');

hf=zeros(2*n-1,5);

hq=[];

for ki=1:n

hf(ki,1)=ki;

hf(ki,2)=input('Please input the frequency: ');

hq=[hq,hf(ki,2)];

end

for ki=n+1:2*n-1

hf(ki,1)=ki;

mhq1=min(hq);

m=size(hq);

m=m(:,2);

k=1;

while k<=m%del min1

if hq(:,k)==mhq1

hq=[hq(:,1:(k-1)) hq(:,(k+1):m)];

m=m-1;

break

else

k=k+1;

end

end

k=1;

while hf(k,2)~=mhq1|hf(k,5)==1%find min1 location

k=k+1;

end

hf(k,5)=1;

k1=k;

mhq2=min(hq);

k=1;

while k<=m%del min2

if hq(:,k)==mhq2

hq=[hq(:,1:(k-1)) hq(:,(k+1):m)];

m=m-1;

break

else

k=k+1;

end

end

k=1;

while hf(k,2)~=mhq2|hf(k,5)==1%find min2 location

k=k+1;

end

hf(k,5)=1;

k2=k;

hf(ki,2)=mhq1+mhq2;

hf(ki,3)=k1;

hf(ki,4)=k2;

hq=[hq hf(ki,2)];

end

clc

choose=input('Please choose what you want:\n1: Encoding\n2: Decoding\n3:.Exit\n');

while choose==1|choose==2

if choose==1

a=input('Please input the letter you want to Encoding: ');

k=1;

while hf(k,2)~=a

k=k+1;

if k>=n

display('Error! You did not input this number.');

break

end

end

if k>=n

break

end

r=[];

while hf(k,5)==1

kc=n+1;

while hf(kc,3)~=k&hf(kc,4)~=k

kc=kc+1;

end

if hf(kc,3)==k

r=[0 r];

else

r=[1 r];

end

k=kc;

end

r

else

a=input('Please input the metrix you want to Decoding: ');

sa=size(a);

sa=sa(:,2);

k=2*n-1;

while sa~=0

if a(:,1)==0

k=hf(k,3);

else

k=hf(k,4);

end

a=a(:,2:sa);

sa=sa-1;

if k==0

display('Error! The metrix you entered is a wrong one.');

break

end

end

if k==0

break

end

r=hf(k,2);

end

choose=input('Choose what you want:\n1: Encoding\n2: Decoding\n3:.Exit\n');

clc;

end

if choose~=1&choose~=2

clc;

end