正方形数

正方形中有几个正方形排列的小点或者圆或者正方形等物体，物体总数就是正方形数。

数学上，平方数，或称完全平方数，是指可以写成某个 整数的 平方的数，即其 平方根为整数的数。例如，9 = 3 × 3，它是一个平方数。

平方数也称正方形数，若 n 为平方数，将 n 个点排成 矩形，可以排成一个 正方形。

若将平方数概念扩展到有理数，则两个 平方数的比仍然是平方数，例如， (2 × 2) / (3 × 3) = 4/9 = 2/3 × 2/3。

若一个整数没有除了 1 之外的平方数为其 因子，则称其为无平方数因数的数。

0也是平方数。

1. 一个 平方数是两个相邻三角形数之和。两个相邻 平方数之和为一个中心正方形数。所有的 奇数 平方数同时也是中心八边 形数。

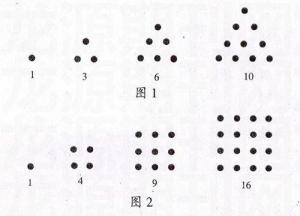2. 四平方和定理说明所有 正整数均可表示为最多四个平方数的和。特别的，三个 平方数之和不能表示形如 4k(8m + 7) 的数。若一个 正整数可以表示因子中没有形如 4k + 3 的素数的奇次方，则它可以表示成两个 平方数之和。

3. 平方数必定不是 完全数。

4. 奇数的平方除以4余1，偶数的平方则能被4整除。

5.a^2-b^2=(a+b)(a-b）

著名数学家毕达哥拉斯发现有趣 奇数现象：将连续奇数相加，每次的得数正好就产生 完全平方数。 如：1 + 3(=2 ) + 5(=3 ) + 7(=4 ) + 9(=5 ) + 11(=6 ) + 13(=7 )……在 奇数和 平方数之间有着密切的重要联系。一个整数是 完全平方数 当且仅当相同数目的点能够在平面上排成一个正方

形的点阵，使得每行每列的点都一样多。

还可以得出式子：1+3+5+7+……+（2n+1）=(n+1)^2

对于一个整数 ，它的 平方写成 。n 等于头 个正 奇数的和（）。在上图中，从1开始，第 个 平方数表示为前一个平方数加上第 个正 奇数，如 5 = 25 = 16 + 9。即第五个 平方数25等于第四个平方数16加上第五个正 奇数：9。

每个 平方数可以从之前的两个平方数计算得到， 递推公式为 n = 2(n − 1) − (n − 2) + 2。例如，2×5 − 4 + 2 = 2×25 − 16 + 2 = 50 − 16 + 2 = 36 = 6 。

平方数还可以表示成 = 1 + 1 + 2 + 2 + ... + n − 1 + n − 1 + n。例如，4 = 16 = 1 + 1 + 2 + 2 + 3 + 3 + 4。可以将其解释为在边长为 3 的矩形上添加宽度为 1 的一行和一列，即得到边长为 4 的矩形。这对于计算较大的数的 平方数非常有用。例如： 52 = 50 + 50 + 51 + 51 + 52 = 2500 + 204 = 2704.