- 一致分布

一致分布
简介
一致分布是外尔(H.Weyl)创始的一个数论分支。
命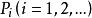 为
为![]() 中的一个点集。对于任意
中的一个点集。对于任意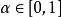 ,若 n 个点
,若 n 个点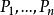 落入区间
落入区间![]() 中的个数
中的个数![]() 满足
满足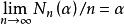 ,则称点集
,则称点集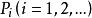 在
在![]() 中一致分布。
中一致分布。
我们称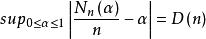 为点集
为点集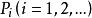 的偏差(discrepancy)。
的偏差(discrepancy)。
判别条件
关于一致分布有次之判别条件:“![]() 中一个数列
中一个数列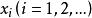 一致分布的充要条件为对于
一致分布的充要条件为对于![]() 中国如何黎曼可积函数
中国如何黎曼可积函数![]() 常有
常有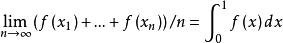 ”。外尓还进一步指出“ 上面判别条件中任何黎曼可积函数可以换成
”。外尓还进一步指出“ 上面判别条件中任何黎曼可积函数可以换成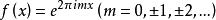 ”。[1]
”。[1]
应用
外尔由一致分布的研究引入了所谓的外尔指数和及其估计。外尔和及其估计是解析数论的核心问题。此外,寻求高维立方体中低偏差的点列,即所谓伪随机数,在高维数值积分、最优化与试验设计中均很有用。
外尔判别法及关于偏差的结果,在s维空间都有相应的推广。
一致分布的定义及外尔判别法还可以推广到紧致空间与拓扑群。
一致分布理论中有不少待解决的问题。例如数列ex(x=1,2,…)是否对模1为一致分布,就是未解决的著名问题。[2][3]

相关百科
-
比亚迪宋Plus 联手博世/采用分布式驱动
2025-09-20 18:57:19 查看详情 -
比亚迪海洋系轿车最新谍照 联手博世/采用分布式驱动
2025-09-20 18:57:19 查看详情 -
比亚迪秦PLUS 联手博世/采用分布式驱动
2025-09-20 18:57:19 查看详情 -
比亚迪海豹正式开启预售 联手博世/采用分布式驱动
2025-09-20 18:57:19 查看详情 -
比亚迪秦PLUS内饰设计图曝光 联手博世/采用分布式驱动
2025-09-20 18:57:19 查看详情 -
nanosox空气分布系统
2025-09-20 18:57:19 查看详情 -
纤维织物空气分布系统
2025-09-20 18:57:19 查看详情 -
分布式计算机控制系统
2025-09-20 18:57:19 查看详情


 求购
求购



