指数幂

1. 同底数幂相乘，底数不变，指数相加。^[3]

即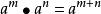(m,n都是有理数)。^[3]

2.幂的乘方，底数不变，指数相乘。^[3]

即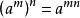(m,n都是有理数)。^[3]

3.积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘。^[3]

即=·(m,n都是有理数)。^[3]

4.分式乘方,分子分母各自乘方。

即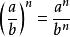(b≠0)。

1. 同底数幂相除，底数不变，指数相减。^[4]

即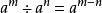(a≠0，m,n都是有理数)。^[4]

2. 规定：

(1) 任何不等于零的数的零次幂都等于1。^[4]

即(a≠0)。^[4]

(2)任何不等于零的数的-p（p是正整数）次幂，等于这个数的p次幂的倒数。^[4]

即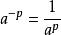(a≠0,p是正整数)。^[4]

（规定了零指数幂与负整数指数幂的意义，就把指数的概念从正整数推广到了整数。正整数指数幂的各种运算法则对整数指数幂都适用。）^[4]

对于乘除和乘方的混合运算，应先算乘方，后算乘除；如果遇到括号，就先进行括号里的运算。^[1]

幂的底数是分数或负数时，底数应该添上^[5]括号，如，。^[1]