- 典范除子

典范除子
中文名
典范除子
所属学科
数学
性质
代数簇上的一类特殊的除子
基本介绍
设![]() 是一个一维代数函数域。
是一个一维代数函数域。
定义1设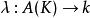 是一个
是一个![]() 线性泛函,如果
线性泛函,如果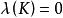 并且存在一个除子D,使
并且存在一个除子D,使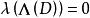 ,则称
,则称![]() 为
为![]() 的一个微分。
的一个微分。
![]()
![]()
![]() 设
设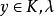 是
是![]() 的一个微分,
的一个微分,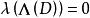 。令
。令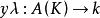 ,是由
,是由 所定义的映射,则
所定义的映射,则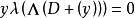 ,故
,故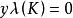 ,故
,故![]() 仍然是的微分。这样,的微分全体形成了一个-向量空间。
仍然是的微分。这样,的微分全体形成了一个-向量空间。
引理1设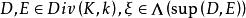 ,则存在
,则存在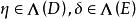 ,使
,使 。
。
引理2设![]() 为
为![]() 的一个非零微分,则存在一个除子D,使
的一个非零微分,则存在一个除子D,使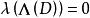 并且对任何满足
并且对任何满足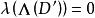 的除子
的除子![]() 都有
都有![]() 。
。
定义2设![]() 为
为![]() 的一个微分,满足引理2中条件的除子D称为
的一个微分,满足引理2中条件的除子D称为![]() 所确定的典范除子,记为
所确定的典范除子,记为![]() [2]。
[2]。
定义3典范除子![]() 是有效除子当且仅当
是有效除子当且仅当
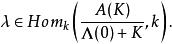
相关定理
引理3K上的微分全体形成的K-空间是一维的。
引理4设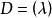 是K的微分
是K的微分![]() 所确定的典范除子,
所确定的典范除子,![]() 是K的一个非零元素,则
是K的一个非零元素,则![]() 等于
等于![]() 。
。
由引理3和引理4立刻可知所有的典范除子都是线性等价的,用![]() 记任何一个典范除子。
记任何一个典范除子。
定理1 黎曼-洛克定理对任何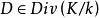 ,都有
,都有
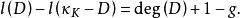
系1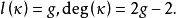



 求购
求购


