- 差分格式

差分格式
差分格式简介
对二阶常微分方程边值问题:
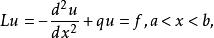 (1)
(1)
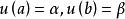 。 (2)
。 (2)
式中,q,f 为 [a,b] 上的连续函数,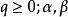 为给定常数。这是最简单的椭圆型方程边值问题。
为给定常数。这是最简单的椭圆型方程边值问题。
将区间 [a,b] 分成 N 等分,分点为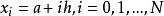 ,其中
,其中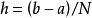 称为步长,
称为步长,![]() 称为网格的节点。于是,得到区间 [a,b] 上的一个网格剖分。
称为网格的节点。于是,得到区间 [a,b] 上的一个网格剖分。
现在将方程 (1) 在节点![]() 离散化。为此,对充分光滑的解 u,由泰勒展式得
离散化。为此,对充分光滑的解 u,由泰勒展式得
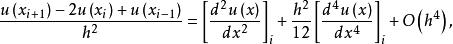 (3)
(3)
其中![]() 表示方括号内的函数 在
表示方括号内的函数 在![]() 点取值。于是在
点取值。于是在![]() 可将方程 (1) 写成
可将方程 (1) 写成
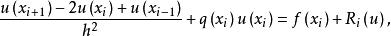 (4)
(4)
其中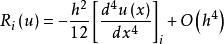 (5)
(5)
显然,当 h 足够小的时候,![]() 是 h 的二阶无穷小量,若舍去
是 h 的二阶无穷小量,若舍去![]() 则得到逼近方程(1)的差分方程:
则得到逼近方程(1)的差分方程:
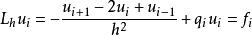 (6)
(6)
式中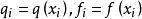 ,称
,称![]() 为差分方程(6)的截断误差。利用差分算子
为差分方程(6)的截断误差。利用差分算子![]() ,可将(4)写成形式
,可将(4)写成形式
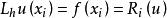 (7)
(7)
而在节点![]() 处,微分方程(1)为
处,微分方程(1)为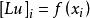 ,以此与(7)相减,得
,以此与(7)相减,得
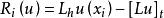 (8)
(8)
所以![]() 是用差分算子
是用差分算子![]() 代替微分算子 L 所引起的截断误差,它关于 h 的阶为
代替微分算子 L 所引起的截断误差,它关于 h 的阶为![]() 。
。
差分方程(6)当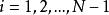 时成立,加上边值条件
时成立,加上边值条件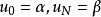 ,就得到关于
,就得到关于![]() 的线性代数方程组:
的线性代数方程组:
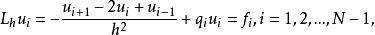 (9)
(9)
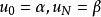 (10)
(10)
它的解![]() 是
是![]() 于
于![]() 的近似。
的近似。
称(9)、(10)为逼近 (1)、(2) 的差分方程或差分格式。
构造方法
构造差分格式的方法有多种,如直接差分化、积分插值法、变分-插分法及待定系数法等。[1]

相关百科
-
差分式同步万向联轴器
2025-11-01 11:10:59 查看详情 -
汽车dvd 大众朗逸车载dvd是什么视频格式
2025-11-01 11:10:59 查看详情


 求购
求购







