各向同性张量

各向同性张量的分量不因坐标系的旋转而改变，即该张量与方向无关。所有零阶张量都是各向同性张量。所有一阶张量都不是各向同性张量。

设、和为任意标量，为克罗内克张量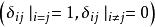，驰为置换张量，则二阶各向同性张量的一般形式为，三阶各向同性张量的一般形式为，四阶各向同性张量的一般形式为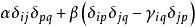。^[1]

一般来说，张量的分量将随坐标变化而变化。例如：在某个坐标系oxyz下的矢量（a，0，0），如果坐标系统绕其z轴选择180°，则在新的坐标系下，该矢量的分量成了（-a，0，0）。可见只要|a|≠0，矢量的分量随坐标系的改变而改变是显而易见的。这类随坐标系改变其分量也随之发生变化的张量成为各向异性张量。反过来，如果存在这样的张量H，其各个分量都不随坐标系的改变而变化，这类张量就称为各向同性张量。比如标量（零阶张量）、克内诺克记号以及置换记号都是各向同性的。各向同性名词来源于物理学。例如，物理学中常用四阶张量来描述有应力作用下的变形状态，即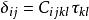，这里称之为拉伸系数。其中分量所表达的物理意义是，在x方向的轴向拉力作用下x方向的拉伸系数。相应的拉伸系数张量就是各向同性张量。

各向同性张量的严格定义可以陈述如下：对于一个n阶张量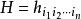，如果它的各个分量在坐标旋转变换下都是不变量，即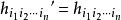，则称之为各向同性张量。一般来说，各向同性张量都满足置换定理。^[2]

在坐标系oxyz的坐标旋转变换中，与原坐标系3个坐标轴重合的变换只有两种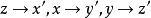，一种是，另一种是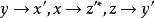，即是说在以上坐标变换下，张量坐标的变换为3→1，1→2，2→3和2→1，1→3，3→2。在这种特点坐标变换下，各向同性张量满足各向同性的定义。即

其中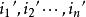，为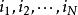按如上之一的置换关系确定的。如上述即为置换定理。

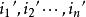置换定理一般陈述是：设为n阶同性张量的某个分量，若另一分量的指标与指标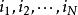满足置换关系，那么必有

各向同性张量的性质主要有以下几点：

(1)零阶张量(标量)都是各向同性张量。

(2)一阶张量除零矢量外都是各向异性。

(3)二阶各向同性张量必为

(4)三阶各向同性张量必为

(5)四阶各向同性张量必为