- 齐次微分方程

齐次微分方程
中文名
齐次微分方程
求解关键
作变换u=y/x,即y=ux
应用学科
高等数学
定义
形如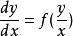 的一阶微分方程称为齐次微分方程,简称微分方程。
的一阶微分方程称为齐次微分方程,简称微分方程。
方程特点
齐次微分方程的特点是其右端项是以![]() 为变元的连续函数。
为变元的连续函数。
例如,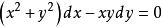 是齐次微分方程,它可以转化为:
是齐次微分方程,它可以转化为: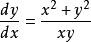 ,即
,即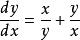 。[1]
。[1]
方程的解
齐次微分方程通过变量代换,可化为可分离变量微分方程来求解。
令![]() 或
或![]() ,
,
其中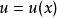 是新的未知函数,对
是新的未知函数,对![]() 两边求导,则有:
两边求导,则有: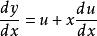 ,
,
将其代入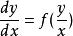 ,得:
,得: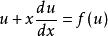 ,
,
分离变量,得: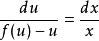
两边积分,得: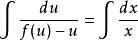 ,
,
求出积分后,再将![]() 回代,便得到方程
回代,便得到方程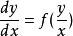 的通解。
的通解。
求解步骤
(1)作变换![]() ,将齐次方程转化为分离变量的微分方程;
,将齐次方程转化为分离变量的微分方程;
(2)求解可分离变量的微分方程;
(3)用![]() 代替步骤(2)中所求通解中的
代替步骤(2)中所求通解中的![]() (即变量还原),就可以得到原方程的通解。[1]
(即变量还原),就可以得到原方程的通解。[1]
注意事项
如果有![]() ,使得
,使得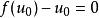 ,则显然
,则显然![]() 也是方程
也是方程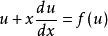 的解,从而
的解,从而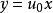 也是方程
也是方程 的解;如果
的解;如果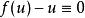 ,则方程
,则方程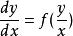 变成
变成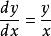 ,这是一个可分离变量微分方程。
,这是一个可分离变量微分方程。
典例
例1
求解方程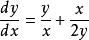 。
。
解:令![]() ,则
,则![]() ,
,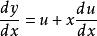 ,
,
原方程变为: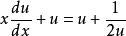 ,即
,即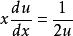 ;
;
分离变量可得: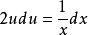 ,
,
左右两端同时积分可得: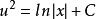 ,
,
将![]() 代入,便可得到原方程的通解为:
代入,便可得到原方程的通解为: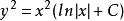 ,其中 C 为任意常数。[1]
,其中 C 为任意常数。[1]
例2
求方程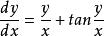 的通解。
的通解。
解:令![]() ,则
,则![]() ,
,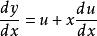 ,
,
原方程变为: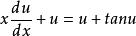 ,即
,即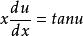 ;
;
分离变量可得: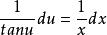 ,
,
左右两端同时积分可得: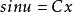 ,
,
将![]() 代入,便可得到原方程的通解为:
代入,便可得到原方程的通解为: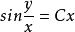 ,其中 C 为任意常数。[2]
,其中 C 为任意常数。[2]

相关百科
-
非线性方程组数值解法
2025-09-28 18:40:16 查看详情 -
F1方程赛车逆向设计
2025-09-28 18:40:16 查看详情 -
三款小排量小型SUV雪铁龙C3 1.8L车型的油耗方程式
2025-09-28 18:40:16 查看详情 -
成都车展:一汽奔腾无限方程架构发布/第三代B70将问世 e
2025-09-28 18:40:16 查看详情 -
雪铁龙C3 1.8L车型的油耗方程式
2025-09-28 18:40:16 查看详情 -
东风雪铁龙凡尔赛C5 1.8L车型的油耗方程式
2025-09-28 18:40:16 查看详情 -
雪铁龙天逸对比大众途岳 1.8L车型的油耗方程式
2025-09-28 18:40:16 查看详情 -
洛特卡-沃尔泰拉方程
2025-09-28 18:40:16 查看详情


 求购
求购





