平行轴定理

平行轴定理能够很简易的，从对于一个以质心为原点的坐标系统的惯性张量，转换至另外一个平行的坐标系统。

对于三维空间中任意一参考点 Q 与以此参考点为原点的直角坐标系 Qxyz ，一个刚体的惯性张量 是

。

这里，对角元素 、 、 分别为对于 x-轴、y-轴、z-轴的惯性矩。设定 为微小质量 对于点 Q 的相对位置。则这些惯性矩，可以精简地用方程定义为

，

，

。

而非对角元素，称为惯性积, 可以定义为

，

，

。

假若已知刚体对于质心 G 的惯性张量 ，质心 G 的位置是 ，则刚体对于原点 O 的惯性张量 ，依照平行轴定理，可以表述为

，

，

，

，

，

。

证明：

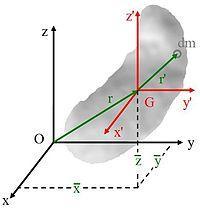惯性张量的平行轴定理

a) 参考右图 ，让 、 分别为微小质量 对质心 G 与原点 O 的相对位置：

， 。

依照惯性张量的惯性矩定义方程，

，

。

所以，

相似地，可以求得 、 的方程。

b) 依照惯性张量的惯性积定义方程 ，

，

。

因为 ， ，所以

相似地，可以求得对于点 O 的其他惯性积方程。

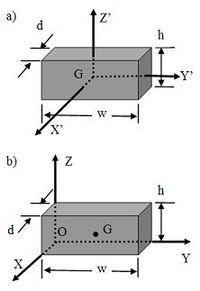实心长方体：a)坐标系统的原点在质心。b)坐标系统的原点在角落。

思考一个实心长方体对于质心 G 的惯性张量，

如图右，质心 G 的位置是 。依照平行轴定理，实心长方体对于点 O 的惯性矩与惯性积分别为

、

、

、

、

、

。

因此，实心长方体对于点 O 的惯性张量是