- 二维分布

二维分布
定义
定义随机变量ξ 和η (有时也称为二维随机向量(ξ,η)的二维(联合)分布函数为:
![]() 不难推知:(ξ,η) 落在矩形区域
不难推知:(ξ,η) 落在矩形区域 上的概率为图(1):
上的概率为图(1):
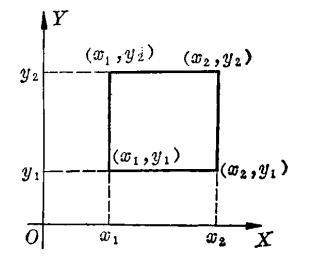 图1
图1


二维分布函数具有以下一些明显的性质:
(1) F(x,y)是x和y的非减函数。
即: ,当
,当
 当
当![]() 。
。
(2) 在-∞处分布函数等于零,即
![]()
(3) 当任一个随机变量的值趋于![]() 时,便得到另一个随机变量的(一维)分布函数。
时,便得到另一个随机变量的(一维)分布函数。
![]()
![]()
![]() 和
和![]() 分别叫做随机变量
分别叫做随机变量![]() 和
和![]() 的边际分布函数。
的边际分布函数。
(4) 当x,y均趋向于﹢∞时,分布函数趋于1。
![]()
下面分别研究通常所遇见的两种类型的随机变量的分布[2]。
离散型二维分布
离散型二维随机变量(D.B.R.V)r=r(X,Y)取值为有限或可列无限的向量(坐标对),则称r(X,Y) 为离散型随机变量[3]
![]() 其分布律为
其分布律为
![]() 则由规范性有
则由规范性有
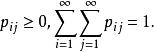 称为随机向量r的分布律,即随机变量X和Y的联合分布律(Joint Distribution),似矩阵的表格显示:
称为随机向量r的分布律,即随机变量X和Y的联合分布律(Joint Distribution),似矩阵的表格显示:
 |
||||||
 |
||||||
 |
||||||
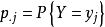 |
 |
连续型二维分布
 |
||||||
 |
||||||
 |
||||||
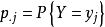 |
 |

相关百科
-
比亚迪宋Plus 联手博世/采用分布式驱动
2025-11-02 07:34:03 查看详情 -
比亚迪海洋系轿车最新谍照 联手博世/采用分布式驱动
2025-11-02 07:34:03 查看详情 -
比亚迪秦PLUS 联手博世/采用分布式驱动
2025-11-02 07:34:03 查看详情 -
比亚迪海豹正式开启预售 联手博世/采用分布式驱动
2025-11-02 07:34:03 查看详情 -
比亚迪秦PLUS内饰设计图曝光 联手博世/采用分布式驱动
2025-11-02 07:34:03 查看详情 -
nanosox空气分布系统
2025-11-02 07:34:03 查看详情 -
纤维织物空气分布系统
2025-11-02 07:34:03 查看详情


 求购
求购


