- 负指数幂

负指数幂
基本简介
在指数法则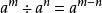 中,如果
中,如果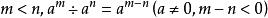 ,则就产生了负指数幂。
,则就产生了负指数幂。
定义负指数幂等于把幂指数变号后所得的幂的倒数。也就是
![]()
应该知道,负指数幂也是不能用正整指数幂的意义来解释的。也就是说“![]() ”不能认为是“
”不能认为是“![]() 个
个![]() 相乘”的意思。另外在定义中规定底数不得为零,其原因是和零指数幂的定义是一样的。
相乘”的意思。另外在定义中规定底数不得为零,其原因是和零指数幂的定义是一样的。
在![]() 中规定,
中规定,![]() ,这是因为
,这是因为![]() 产生于
产生于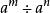 , 当
, 当![]() 时,
时,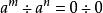 ,我们知道0是不能作除数的, 所以
,我们知道0是不能作除数的, 所以![]() 中,当
中,当![]() 时,
时,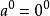 这是没有意义的[2]。
这是没有意义的[2]。
相关概念
幂
n个![]() 相乘的积称为“
相乘的积称为“![]() 的n次幂”或“
的n次幂”或“![]() 的n次乘方”记作
的n次乘方”记作![]() ,
,![]() 是底数,n是指数。这里n可以是分数、负数,分别称为“分指数幂”、“负指数幂”,也可以是任意实数或复数。
是底数,n是指数。这里n可以是分数、负数,分别称为“分指数幂”、“负指数幂”,也可以是任意实数或复数。
分指数幂
当幂的指数为分数时,称为“分指数幂”。正数![]() 的
的![]() 次幂(
次幂(![]() 是既约正分数)定义为
是既约正分数)定义为![]() 的m次幂的n次算术根,就是:
的m次幂的n次算术根,就是:
![]()
乘方
(1)n个![]() 相乘的积
相乘的积![]() 称为
称为![]() 的n次“乘方”,参见“幂”。
的n次“乘方”,参见“幂”。
(2)从![]() 求
求![]() 的运算,称为“乘方”。
的运算,称为“乘方”。
正整数指数幂
一般地,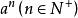 叫作
叫作![]() 的
的![]() 次幂,
次幂,![]() 叫作幂的底数,
叫作幂的底数,![]() 叫作幂的指数,并且规定
叫作幂的指数,并且规定![]() 。我们注意到在
。我们注意到在![]() 的n次幂定义中,n是正整数,因此通常又把它称为正整数指数幂[3]。
的n次幂定义中,n是正整数,因此通常又把它称为正整数指数幂[3]。
容易验证,正整数指数幂的运算满足如下法则:
(1)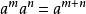 ;
;
(2)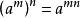 ;
;
(3)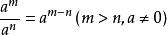 ;
;
(4)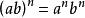 。
。
负整数指数幂
在法则(3)中规定了![]() ,如果取消这个限制,就需要讨论下面两种情形:
,如果取消这个限制,就需要讨论下面两种情形:
❶当![]() 时,幂的商有如下运算:
时,幂的商有如下运算:
![]() 依照法则(3)则有
依照法则(3)则有
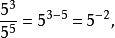 即
即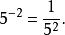
这就说明当指数为负整数时,幂的值是有意义的。此时规定
![]()
![]() 叫作负整数指数幂。
叫作负整数指数幂。
零指数幂
❷当![]() 时,幂的商有如下运算:
时,幂的商有如下运算:
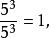 且
且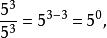 故
故![]()
这说明当指数为零时,幂的值是有意义的。此时规定
![]()
![]() 叫作零指数幂,又叫零次幂。但是
叫作零指数幂,又叫零次幂。但是![]() 是无意义的。
是无意义的。
正整数指数幂、负整数指数幂、零指数幂统称为整数指数幂。正整数指数幂的运算法则对整数指数幂仍然是成立的。特别地,有[3]
![]()
![]()
整数指数幂的运算法则
同上所述,容易验证,正整数指数幂的运算满足如下法则:
(1)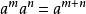 ;
;
(2)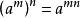 ;
;
(3)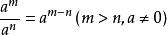 ;
;
(4)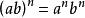 。
。
(5)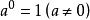 ;
;
注:①这些运算性质在整数指数范围内仍然适用。
②任何不等于零的数的![]() (n为正整数)次幂,等于这个数的n次幂的倒数,即
(n为正整数)次幂,等于这个数的n次幂的倒数,即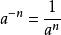 (
(![]() ,n为正整数)。在这两个幂的意义中,强调底数
,n为正整数)。在这两个幂的意义中,强调底数![]() 都不等于零,否则无意义。
都不等于零,否则无意义。
③学习了零指数幂和负整数指数幂后,正整数指数幂的运算性质可以推广到整数指数幕的范围[2]。
幂的运算法则
当指数概念扩充到任意实数之后,幂的运算法则可合并为[4]:
(1)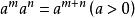 ;
;
(2)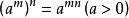 ;
;
(3)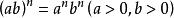 。
。

-
截断二进制指数退避算法
2025-09-15 10:33:13 查看详情 -
如何查询汽车价格定基指数 定基价格指数的概述
2025-09-15 10:33:13 查看详情


 求购
求购







