仿射不变量

给定一组多项式，设是由这组多项式的系数所决定的函数，G是作用在这些系数上的变换群，如果经过变换群G作用后函数值不变，就称为这组多项式或由这组多项式所组成的方程组在变换群G作用下的不变量(invariant)。当G分别代表运动群、仿射群和射影群时，相应的不变量称为“度量不变量”、“仿射不变量”和“射影不变量”。例如， 在平面上，关于坐标x、y的二次方程

在运动群G作用下有三个度量不变量：

其中记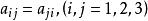，在平面直角坐标系中上述二次方程代表,一条二次曲线，也称为二次曲线的度量不变量，按照它们的符号，能够对二次曲线作出度量分类，寻找和研究不变量，是几何学中一个重要的问题^[2]。

分比(proportion by subtraction)亦称“单比”，直线上三点P1、P2、P3的分比是。分比是仿射不变量，而且是基本不变量，即：任一仿射不变量都可用分比的一个函数来表达^[2]。

图形经过任何仿射变换后都不变的性质(量)，称为图形的仿射性质(仿射不变量)。

注：同素性，结合性，平行性和共线三点单比不变是基本的仿射性质。

有关仿射性质的一些定理和推论：

定理1两条平行直线经过仿射变换后仍变为两条平行直线。

推论1两条相交直线经过仿射变换后仍变为两条相交直线。

推论2共点直线经仿射变换后，仍变为共点直线。

定理2两条平行线段之比是仿射不变量.

定理3两个三角形面积之比是仿射不变量。

推论1两个多边形面积之比是仿射不变量。

推论2两个封闭图形面积之比是仿射不变量^[3]。

例1 两条平行线段之比是仿射不变量^[3]。

证明 设线段AB平行于线段CD，经过仿射变换后，其对应线段A'B'C'D'互相平行，下面我们只须证明

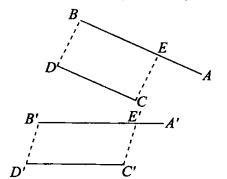图1

如图1所示连接BD，作CE // BD交AB于E。由于仿射变换保持结合性和平行性，所以E的对应点E'在A'B'上，且C'E' // B'D'，又因为仿射变换保持共线三点的单比，所以有

即

而

所以

综上所述，两条平行线段之比经仿射变换后不变^[3]。