- 保角映射

保角映射
概念
设函数w=f(z)在区域D内解析,![]() 且
且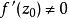 .过点
.过点![]() 任意引一条有向光滑曲线
任意引一条有向光滑曲线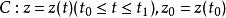 且
且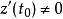 ,则曲线C在点
,则曲线C在点![]() 处的切线存在,其倾角为
处的切线存在,其倾角为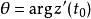 .
.
映射w=f(z)把z平面内的曲线C映射成![]() 平面内过点
平面内过点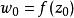 的一条有向光滑曲线
的一条有向光滑曲线
![]() 由于
由于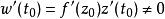 .故曲线
.故曲线![]() 在点
在点![]() 处切线存在.其倾角为
处切线存在.其倾角为
![]()
上式表明,象曲线![]() 在
在![]() 的切线方向可由曲线C在
的切线方向可由曲线C在![]() 处的切线方向旋转一个角度
处的切线方向旋转一个角度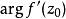 得出.称
得出.称 为函数w=f(z)在点
为函数w=f(z)在点![]() 处的旋转角.显然,
处的旋转角.显然,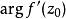 只与
只与![]() 有关,与过点
有关,与过点![]() 的曲线C的形状无关,这一性质称为旋转角的不变性.
的曲线C的形状无关,这一性质称为旋转角的不变性.
由于映射w=f(z)使所有经过点![]() 的曲线都旋转同一个角度,所以相交于点
的曲线都旋转同一个角度,所以相交于点![]() 的任意两条曲线
的任意两条曲线![]() 和
和![]() 的夹角,其大小和方向都等于映射后的象曲线
的夹角,其大小和方向都等于映射后的象曲线![]() 和
和![]() 的夹角,如图1所示,这一性质称为保角性.
的夹角,如图1所示,这一性质称为保角性.
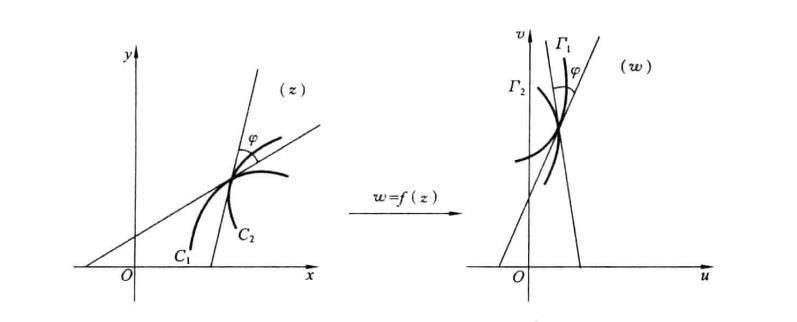 图1
图1
假设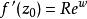 ,则
,则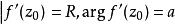 ,于是
,于是
![]()
上式表明在点![]() 的某邻域内自变量改变量的模
的某邻域内自变量改变量的模![]() 和函数值改变量的模
和函数值改变量的模![]() 在忽略高阶无穷小的情况下有关系式
在忽略高阶无穷小的情况下有关系式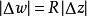 ,即在点
,即在点![]() 附近象曲线伸长到原象曲线的R倍。R反映了在映射w=f(z)下,z平面上C曲线在点
附近象曲线伸长到原象曲线的R倍。R反映了在映射w=f(z)下,z平面上C曲线在点![]() 处弧长的伸缩率,这是导数模的几何意义;并且伸缩率
处弧长的伸缩率,这是导数模的几何意义;并且伸缩率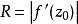 ,它仅与点
,它仅与点![]() 有关,而与过点
有关,而与过点![]() 的曲线C的形状、方向无关,这一性质称为伸缩率的不变性,
的曲线C的形状、方向无关,这一性质称为伸缩率的不变性,
综上所述,可得定理1,
定理1: 设函数w=f(z)在区域D内解析,![]() 为D内的一点,且
为D内的一点,且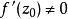 ,则映射w=f(z)在点
,则映射w=f(z)在点![]() 处具有:
处具有:
(1)保角性,即过点![]() 的两条曲线问的夹角与映射后所得两曲线间的夹角在大小和方向上保持不变;
的两条曲线问的夹角与映射后所得两曲线间的夹角在大小和方向上保持不变;
(2)伸缩率不变性,即通过点![]() 的任何一条曲线的伸缩率均为
的任何一条曲线的伸缩率均为![]() ,而与曲线的形状和方向无关。
,而与曲线的形状和方向无关。
若函数w=f(z)在点![]() 的邻域内有定义,且在点
的邻域内有定义,且在点![]() 处具有:
处具有:
(1)保角性:
(2)伸缩率的不变性;
则称映射w=f(x)在点![]() 处是保角的。
处是保角的。
若映射w=f(z)在区域D内的每一点都是保角的,则称w=f(z)是区域D内的保角映射。
可知,若函数w=f(z)在区域D内解析,且对任意点![]() ,有
,有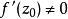 ,则w=f(z)在D内是保角映射。[1]
,则w=f(z)在D内是保角映射。[1]
几种简单的保角映射
1.分式线性映射
定义: 形如
![]() 的映射称为分式线性映射.其中a、b、c、d是复常数.而且
的映射称为分式线性映射.其中a、b、c、d是复常数.而且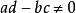 .
.
当c=0时,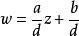 .
.
当![]() 时,
时,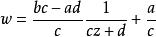 .
.
分式线性映射可以分解为如下基本形式的映射:
![]() 因此,分式线性映射可以看作是
因此,分式线性映射可以看作是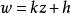 和
和![]() 两种映射的复合.
两种映射的复合.
例如,z平面上以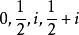 为顶点的长方形,经过保角映射
为顶点的长方形,经过保角映射
![]() 变换成
变换成![]() 平面上以2-i,3,i,1+2i为顶点的长方形,其变换过程如图2所示.
平面上以2-i,3,i,1+2i为顶点的长方形,其变换过程如图2所示.
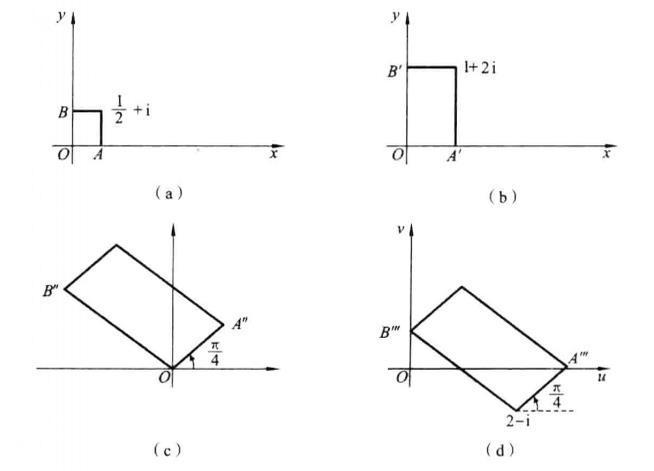 图2
图2
可见,整式线性映射是不改变图形相似形状的变换,它在整个复平面上是处处保角、一一对应的.又由于该映射能把z平面上的圆周映射成训平面上的圆周,所以这一性质称为整式线性映射的保圆性.
映射![]() 称为倒数映射,它也是保角映射.
称为倒数映射,它也是保角映射.
2.指数函数![]() 所确定的映射
所确定的映射
由于![]() 在复平面内处处解析,且
在复平面内处处解析,且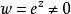 ,所以指数函数
,所以指数函数![]() 所确定的映射是保角映射.
所确定的映射是保角映射.
又由于![]() 以
以![]() 为周期,所以只需讨论当z在由
为周期,所以只需讨论当z在由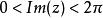 所定义的带形区域B中变化时,函数
所定义的带形区域B中变化时,函数![]() 的映射性质.
的映射性质.
设![]() 的实部及虚部分别为u及v,在带形区域B中,z从左向右描出一条直线
的实部及虚部分别为u及v,在带形区域B中,z从左向右描出一条直线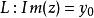 ,如图3所示,则
,如图3所示,则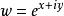 ,于是
,于是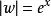 从0(不包括0)增大到
从0(不包括0)增大到![]() .而
.而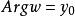 保持不变。所以,
保持不变。所以,![]() 描出一条射线
描出一条射线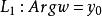 (不包括0),如图3(b))所示。
(不包括0),如图3(b))所示。
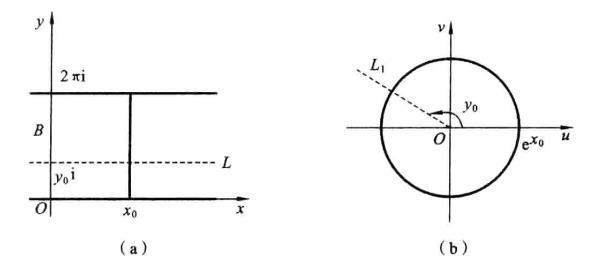 图3
图3
指数函数![]() 确定了从带形区域B:
确定了从带形区域B: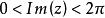 到
到![]() 平面除去原点和正实轴的保角映射.可见
平面除去原点和正实轴的保角映射.可见![]() 将
将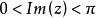 保角映射为上半平面
保角映射为上半平面 ;而把
;而把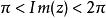 保角映射为下半平面
保角映射为下半平面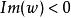 .
.
映射![]() 的特点是:将扩充z平面上的水平带形区域
的特点是:将扩充z平面上的水平带形区域 映射成扩充
映射成扩充![]() 平面的角形区域
平面的角形区域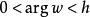 (
(![]() 时,此角形区域为上半平面).[1]
时,此角形区域为上半平面).[1]

-
奥迪a6l如何连手机映射
2025-11-01 10:45:38 查看详情


 求购
求购






