聚点

任给，存在无穷多个满足

则称为复数序列的一个聚点。^[3]

有的序列可以有多个聚点。例如，实数序列

就有两个聚点1和-1.当序列的极限存在时，序列的极限是此序列的唯一聚点。^[4]

在实数序列中，数值最大的聚点称为的上极限，记作

数值最小的聚点称为的下极限，记作

对于上述序列

上极限与下极限的概念在计算级数收敛半径时常会用到。^[3]

a是X的聚点的充要条件是：存在X中的各项不同的数列，使得^[4]

事实上，只要证明在且的数列中，可以选出各项不同的子数列就可。因为且，这说明该数列不可能只有有限多个不同项组成(否则必有一项的值在中无穷次出现，这样就收敛到该值，而它又不等于a，从而得出矛盾)，取这些不同项，按原来的顺序排列后所得数列就是定理所要求的数列。

例给出以[0，1]上所有实数为聚点的数列。^[4]

解利用(0，1)上的有理数集的聚点就是[0，1]这个事实，来

构造数列如下：

当然上述数列的项有相同的，如果舍去和前面相同的项的话，就得到一个各项不同的数列，它以[0，1]上实数为聚点，而各项又都是有理数。

（维尔斯特拉斯聚点定理）任何有界的无穷数集，都有聚点存在。^[4]

(波尔察诺定理) 有界数列有收敛的子数列。

证明若数列有无穷多项相同，它们重复出现的序号为

则就是一个收敛的子数列。若没有无穷多项相同，则数集为无穷有界数集，则由聚点原理，必有聚点a存在。再由定理1，在数集中有一个数列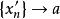，a，以的次序排列后，得的一个子数列，它以a为极限，其中用了收敛数列重排后极限不变。^[4]