聚点定理

定义1（经典含义）：设S为数轴上的点集，ξ为定点（它可以属于S，也可以不属于S）。若ξ的任何ε邻域内都含有S中的无穷多个点，则称ξ为点集S的一个聚点。

定义2（拓扑含义）：对于点集S，若点ξ的任何ε邻域内都含有S中的异于ξ的点，或点ξ的任何ε去心邻域内都含有S中的点，则称ξ为S的一个聚点。

定义3（极限含义）：对于点集S，如果在S中存在一个各项互异且收敛的数列{xn}，则{xn}的极限ξ为S的一个聚点。

这些定义在数轴上是等价的，即互为充要条件，但是这些定义稍有不同，具体的不同稍后会提及。

聚点定理经典形式：实轴上的任一有界无限点集S至少有一个聚点。

聚点定理一般形式：列紧空间的任何序列都含有收敛子列（继而含有聚点，但是这个聚点不一定还在这个空间中）。

由于聚点定理反应了实数的完备性，故由实数公理——戴德金定理进行证明。

已知S是数轴上一有界无限点集，即S⊆[a,b]。

设有一个实数集A，A中的任一元素c满足：区间中最多有S中的有限项，而S中的无限项都落在。

并把A在R中的补集设为B，则：

①显然，因此，A、B都非空。

②。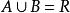

③根据数集A的定义，。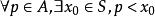

又根据数集B的定义，。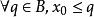

∴必有。

由戴德金定理得，存在唯一实数η是A、B的分界点，并且要么η是A中的最大值，要么η是B中的最小值。

如果η是A中的最大值，那么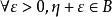。由于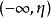上仅有S中的有限个点，故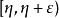上有S中的无数个点。否则，如果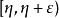只有S中的有限个点，那么因为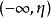上仅有S中的有限个点，所以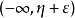上也仅有S中的有限个点。这样一来就导致，矛盾。根据聚点的定义，η为S的聚点。

如果η是B中的最小值，那么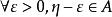，因此在区间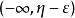上仅有S中的有限个点。那么在区间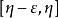上就有S中的无数个点。否则，如果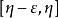上只有S中的有限个点，那么因为区间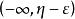上仅有S中的有限个点，所以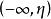上也仅有S中的有限个点。这样一来就导致，与η是B中的最小值矛盾。根据聚点的定义，η为S的聚点。

致密性定理：有界数列必有收敛子列。

致密性定理和聚点定理是等价的，可以由聚点定理直接推出致密性定理（当然也可以由致密性定理推出聚点定理），因此有的书上把致密性定理作为聚点定理的推论来介绍。但由于致密性定理和聚点定理一样，都反应了实数的连续性，所以依然可以用实数公理来进行推导。

以下给出一个聚点定理推出致密性定理的步骤。

若有界数列中含有无数个相同的项，取这些相同的项构成的一个子列，则该子列为常数列，而常数列总是收敛的。

假设有界数列中不含有无数个相同的项，则对应在数轴上为一有界无限点集。根据聚点定理，中存在聚点C。于是按照聚点的定义3，存在一个的子列，该子列收敛到C。

牛顿和莱布尼兹创立了微积分，但是当时分析的基础还极其不完善，这导致了第二次数学危机，直接的结果就是大量优秀的数学家投身到了研究实数基础的行列中，这其中相当重要的一部分就是实数的完备性公理，实数的完备性公理包括六条，这六条是等价的，而维尔斯特拉斯聚点定理就是其中的一条。

1817年，致密性定理作为证明介值定理的引理第一次被波尔查诺证明。过了50多年后，其等价命题——聚点定理被发现并由维尔斯特拉斯证明。自此以后，波尔查诺-维尔斯特拉斯定理作为数学分析的一条基本定理被广泛运用起来。

作为分析学早期的经典定理之一，维尔斯特拉斯定理成为了分析的基础，是研究实数的几何性质的重要工具，后来，因为它是很多拓扑空间所共有的性质，终于使数学家修正了聚点的原始定义，赋予它拓扑含义，进而建立了列紧性的概念，所谓列紧性就是指：对于距离空间X中的集合M，M的任何序列都含有一个收敛的子序列（这个子序列的极限未必还在M中），列紧性成为衡量距离空间“好坏”的一个重要标准，是研究距离空间的重要几何概念，维尔斯特拉斯聚点定理的推广也可以称为数学定理公理化的一次完美的实践。

作为聚点定理应用的一个例子，上面已经给出了证明致密性定理的方法。接下来再举一个例子，采用聚点定理来证明单调有界定理。

已知{xn}是一单调递增且有上界的数列，求证当n→∞时，{xn}收敛。

证明：因为{xn}单调递增，故x1是其一个下界。又因为{xn}有上界，所以{xn}有界。

由n→∞且{xn}有界可知，此时{xn}是一有界无限点集。根据聚点定理，{xn}存在一个聚点ξ。

由聚点的定义可知，对任意ε>0，区间(ξ-ε,ξ+ε)内含有{xn}的无数个点。又因为{xn}是单调递增的，从而存在正整数N，当n>N时，这无数个点都落在区间(ξ-ε,ξ+ε)内，而只有有限个（最多N个）点落在(ξ-ε,ξ+ε)外。

根据极限的几何意义，{xn}收敛到ξ，这就证明了单调递增且有上界的数列必有极限。

同理可证单调递减且有下界的数列必有极限。