- 等号

等号
基本简介
 等号若
等号若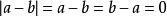 ,则a=b。
,则a=b。
数学符号: "="。
解释:当一个数值与另一个数值相等时,使用等于号"="表示。
举例:a=3,b=3,a与b相等。即a=b (a等于b)。
“=”表示两边的地位等都是一样的,例如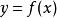 ,在这里边y 就是f(x) ,f(x)就是y,两边的地位是一样的[2]。
,在这里边y 就是f(x) ,f(x)就是y,两边的地位是一样的[2]。
历史沿革
在15、16世纪的数学书中,还用单词代表两个量的相等关系。例如在当时一些公式里,常常写着aequ或aequaliter这种单词,其含义是“相等”的意思。1557年,英国数学家列科尔德,在其论文《智慧的磨刀石》中说:“为了避免枯燥地重复isaequalleto(等于)这个单词,我认真地比较了许多的图形和记号,觉得世界上再也没有比两条平行而又等长的线段,意义更相同了。”于是,列科尔德有创见性地用两条平行且相等的线段“=”表示“相等”,“=”叫做等号。用“=”替换了单词表示相等是数学上的一个进步。由于受当时历史条件的限制,列科尔德发明的等号,并没有马上为大家所采用。
历史上也有人用其它符号表示过相等。例如数学家笛卡儿在1637年出版的《几何学》一书中,曾用“∞”表示过“相等”。直到17世纪,德国的数学家莱布尼兹,在各种场合下大力倡导使用“=”,由于他在数学界颇负盛名,等号渐渐被世人所公认[3]。
相关拓展
把“>”,“=”这两个符号有机地结合起来,得到符号“≥”,当一个数值比另一个数值大或两数相等时,使用大于等于号"≥",读作“大于或等于”,有时也称为“不小于”。对于任意两实数a,b,都可在同一数轴上找到其对应点A,B。若点A在点B右侧或A与B重合,则a≥b。
同样,把“<”,“=”这两个符号有机地结合起来,得到符号“≤”,读作“小于或等于”,有时也称为“不大于”。小于等于是一种判断方式,用来表示不等式左侧的值小于等于不等式右侧的值,经常在各种数学或编程中出现。在命题中,小于等于是小于或者等于,只要满足一个条件即可成立。
不等号:“≠”是表示“不相等”关系的符号。“≠”和“=”的意义相反,在数学里也经常用到,例如a+1≠a+5[2]。
教学应用
等号“=”是数学中等式运算符号。广泛运用在算数中,是小学必学的内容。要培养学生的符号感,就必须树立符号意识,有目的、有意识、有计划、有步骤地渗透于数学教学的始终。在一年级“认数”单元,要注意加强对数的实际意义的理解,在认识了1--5以后,教学几和第几的认识,让学生联系生活经验,体会一个数可以用来表示物体的个数,也可以用来表示物体排列的顺序。还要十分重视帮助学生建立数的大小概念,把握数的大小关系。在教学“=”、“>”、“<”的认识时,可以采用模拟童话场景的方式,如“森林运动会”,从不同动物只数的比较中,抽象出数的大小关系。比较两种物体数量的多与少,基本方法是一一对应、数形结合。通过一一对应的排列让学生明确它们的只数,以此建立“同样多”的概念,在此基础上用数形结合的方法抽象出“4 =4",认识并理解“=”的含义,使学生知道,当两个物体个数“同样多”时,可以用“=”来表示。由此可见,符号意识的培养需要坚实的经验为基础,在教学中应促进学生在交流、分享的过程中积累经验,学习符号化的多种途径,允许个性化地表示符号;逐步体会用数、形将实际问题“符号化”的优越性,感受符号在理解和解决问题过程中的价值[2]。
例题
在下列()中填写“=”、“>”、“<”[4]。
a)12()13-1
b)4*4()5*30
c)10()9*1+1
答案:
a)“=”;
b)“<”;
c)“=”。



 求购
求购

