- 大于

大于
基础定义
解释:当一个数值比另一个数值大时使用大于号">".
其几何意义可以这样解释:
对于任意两实数a,b,都可在同一数轴上找到其对应点A,B
若点A在点B右侧,则a>b
举例:a=3,b=1,a比b大。即a>b (a大于b)
定义
若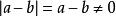 ,则
,则![]() ;反之,若
;反之,若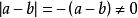 ,则
,则![]()
应用举例
在下列()中填写“=”、“>”、“<”。
a)2()3
b)4*4()5*3
c)10()100-9*9
答案:a)“<”;b)“>”;c)“<”;
数学符号
大于号‘>’是数学中不等式运算符号的一种。大于号被广泛运用在算数中,是小学必学的内容。
英国人哈里奥特于1631年开始采用现今通用之“大于”号“>”及“小于”号“<”,但并未为当时数学界所接受。直至百多年后才渐成标准之应用符号。
庞加莱与波莱尔于1901年引入符号<<(远小于)和>>(远大于),很快为数学界所接受,沿用至今。
其他不等式符号
小于号“<”是数学中不等式运算符号的一种。是英国数学家哈利奥特在自己的《使用分析学》(Artis Analyticae Praxis)一书中首先使用了“<”和“>”符号,但是直到他去世十年之后1631年才发表。a<b,表示a的数值比b的数值小。[2]
大于等于的数学符号为≥。当一个数值比另一个数值大或两数相等时使用大于等于号"≥",又被称为“不小于”。对于任意两实数a,b,都可在同一数轴上找到其对应点A,B。若点A在点B右侧或A与B重合,则a≥b。
小于等于是一种判断方式,用来表示不等式左侧的值小于等于不等式右侧的值,符号为“≤”。例如3≤5。在各种数学,或编程中会出现。命题中,小于等于是小于或者等于,只要满足一个条件即可成立。小于等于又称为不大于。[3]
相关教学
培养学生的符号感,就必须树立符号意识,有目的、有意识、有计划、有步骤地渗透于数学教学的始终。在一年级“认数”单元,教材十分注意加强对数的实际意义的理解,在认识了1--5以后,教学几和第几的认识,让学生联系生活经验,体会一个数可以用来表示物体的个数,一也可以用来表示物体排列的/顷序。教材还十分重视帮助学生建立数的大小概念,把握数的大小关系。在教学“=”“>”“<”的认识时,例题提供了童话场景“森林运动会”,从不同动物只数的比较中,抽象出数的大小关系。比较两种物体数量的多与少,基本方法是一一对应、数形结合。通过一一对应的排列让学生明确它们的只数,以此建立“同样多”的概念,在此基础上用数形结合的方法抽象出“4 =4",认识并理解“=”的含义,使学生知道,当两个物体个数“同样多”时,可以用“=”来表示。接着引导学生比较运动会上松鼠和小熊的只数,通过一一对应的排列,使学生明确松鼠只数比小熊多,小熊只数比松鼠少,从而建立“多”“少”的概念,并以此为基础还用数形结合的方法抽象出“5 >3”和“3 <5",认识理解“>”“<”的含义,学会用“>”“<”表示两数之间的关系。由此可见,符号意识的培养需要坚实的经验为基础,在教学中应促进学生在交流、分享的过程中积累经验,学习符号化的多种途径,允许个性化地表示符号;逐步体会用数、形将实际问题“符号化”的优越性,感受符号在理解和解决问题过程中的价值。[4]

-
我的心略大于整个宇宙
2025-09-28 09:26:47 查看详情


 求购
求购




