中垂线

　　经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）（英文：perpendicular bisector）。垂直平分线，简称“中垂线”，是初中几何学科中占有绝大部分的非常重要的一部分。

有A,B,C(不在同一条直线上)三个村庄，现要准备建一所学校，要求学校到三个村庄的距离相等，请确定学校的位置。

解析：依次连接AB,AC,BC，作AB,BC的垂直平分线，交于一点O，则由垂直平分线性质有OA=OB，OB=OC，故OA=OB=OC，O即为学校的位置。^[1]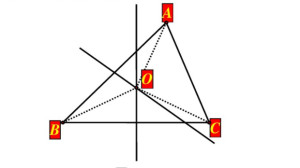中垂线

(1)垂直平分线垂直且平分其所在线段；

(2)垂直平分线上任意一点，到线段两端点的距离相等；

(3)三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等；

(4)垂直平分线的判定：必须同时满足（1）直线过线段中点;（2）直线⊥线段。

逆定理：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

如图1，已知N是AB中点，MN是AB的垂直平分线，平面上一点P满足PA=PB，证明：P在MN上。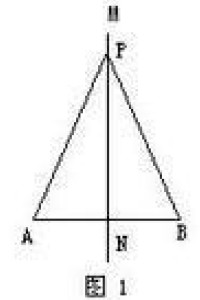中垂线

解：

∵MN是AB的垂直平分线

∴AN=BN

∵PA=PB ，PN=PN

∴△PAN≌△PBN

∴∠PNA=∠PNB

∵∠PNA+∠PNB=180°

∴∠PNA=∠PNB=90°

由于过平面上一点，有且仅有一条直线与已知垂线垂直，故P在MN上。

该逆定理得证。

尺规作图法

度量法

折纸法（折叠法）

方法一：（用圆规作图） 　　

1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。 　　

2、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线。得到一个交点(两交点交与线段的同侧)。 　　

3、连接这两个交点。 　　原理：等腰三角形的高垂直等分底边。 　　

方法二： 　　1、连接这两个交点。 原理：两点成一线。 　　

等腰三角形的性质： 　　1、三线合一(　等腰三角形底边上的高线、底边上的中线、顶角平分线相互重合。 ) 　　2、等角对等边 　　3、等边对等角

方法三：分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线，得到两个交点(两交点交于线段的两侧)

①利用定义：经过某一条线段的中点，并且垂直于这条线段的直线是线段的垂直平分线；

②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．（即线段垂直平分线可以看成到线段两端点距离相等的点的集合）。

若图形（这个图形可以是直线的、折线的、曲线的）关于某条直线对称，这条轴就称为对称轴。以五角星为例，它有五条对称轴。

垂直平分线是存在某条线段时才会有这个概念。它的定义是经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）。它有一定的局限性。

轴对称图形的对称轴是对称图形中任意两个对应点连线段的垂直平分线。