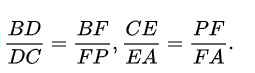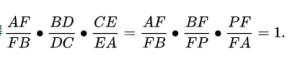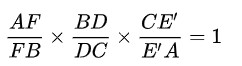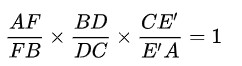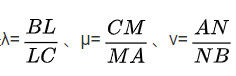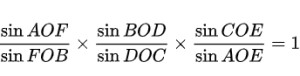梅涅劳斯定理

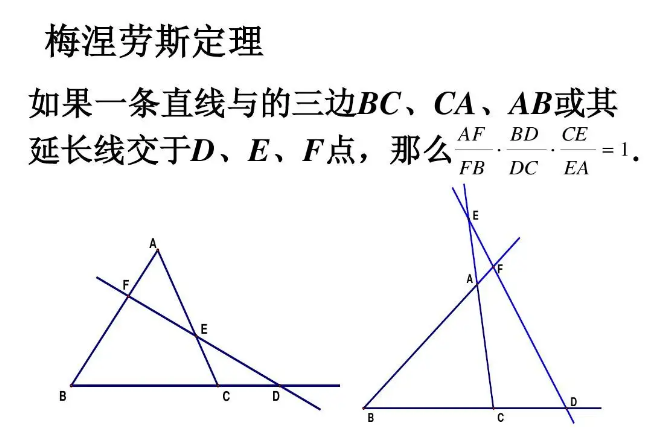梅涅劳斯定理(3)当一条直线交三边所在的直线分别于点时，则有

过点A作AG∥DF交BC的延长线于点G.则

公式

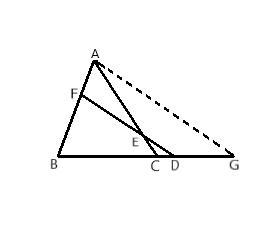证明一

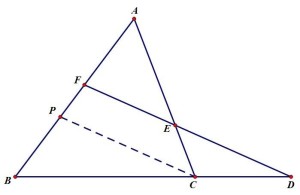插图过点C作CP∥DF交AB于P，则公式

两式相乘得公式

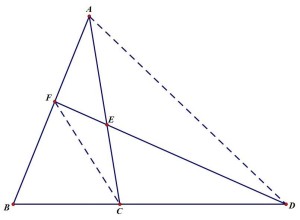插图连结CF、AD，根据“两个三角形等高时面积之比等于底边之比”的性质有。

AF：FB =S△ADF：S△BDF…………（1），

BD：DC=S△BDF：S△CDF…………（2），

CE：EA=S△CDE：S△ADE=S△FEC：S△FEA=（S△CDE+S△FEC

）：（S△ADE+S△FEA）

=S△CDF：S△ADF………… （3）

（1）×（2）×（3）得

公式

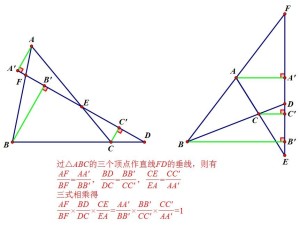插图

过三顶点作直线DEF的垂线AA‘，BB'，CC'，如图：

充分性证明：

△ABC中，BC，CA，AB上的分点分别为D，E，F。

连接DF交CA于E'，则由充分性可得，公式

又∵公式

∴有CE/EA=CE'/E'A，两点重合。所以共线

推论在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是公式

于是L、M、N三点共线的充要条件是λμν=-1。（

注意与塞瓦定理相区分，那里是λμν=1）^[2]

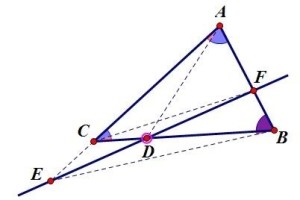插图此外，用该定理可使其容易理解和记忆：

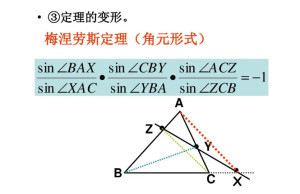
第一角元形式的梅涅劳斯定理如图：若E，F，D

三点共线，则公式

即图中的蓝角正弦值之积等于红角正弦值之积。

该形式的梅涅劳斯定理也很实用。

证明：可用面积法推出：第一角元形式的梅氏定理与顶分顶形式的梅氏定理等价。

第二角元形式的梅涅劳斯定理

在平面上任取一点O，且EDF共线，则公式

(O不与点A、

插图

B、C重合)

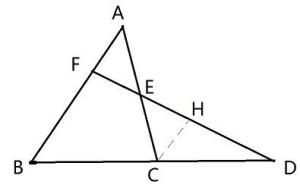插图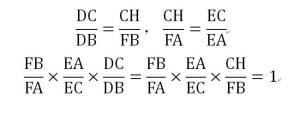公式作CH平行于AB交FD于点H

梅涅劳斯定理(3)使用梅涅劳斯定理可以进行直线形中线段长度比例的计算，其逆定理还可以用来解决三点共线、三线共点等问题的判定方法，是平面几何学以及射影几何学中的一项基本定理，具有重要的作用。梅涅劳斯定理的对偶定理是塞瓦定理。^[3]

它的逆定理也成立：若有三点F、D、E分别在三角形的边AB、BC、CA或其延长线上，且满足AF/FB×BD/DC×CE/EA=1，则F、D、E三点共线。利用这个逆定理，可以判断三点共线。

若梅氏线完全在三角形外，那么该三角形仍然成立。

顶点到交点，交点回顶点。