米氏常数

　　非竞争性抑制剂米氏常数不变，最大反应速度减小；竞争性抑制剂米氏常数增大而，最大反应速度不变。

　　Km：米氏常数，是研究酶促反应动力学最重要的常数。

在20世纪初期，就已经发现了酶被其底物所饱和的现象，而这种现象在非酶促反应中，则是不存在的，后来发现底物浓度的改变，对酶反应速度的影响较为复杂，1913年前后Michaelis和Menten作了大量的定量研究，积累了足够的实验证据，从酶被底物饱和的现象出发，按照中间产物设想，提出了酶促反应动力学的基本原理，并归纳为一个数学表达式，称之为米氏方程式：

[E]+[S]↔[ES]↔P+[E]

v=Vm[s]/(Km+[s])=Vm/(1+Km/[s])

式中，[E]为游离酶浓度；[S]为底物浓度；[ES]为酶与底物结合的中间络合物浓度；v为酶促反应速度；Vm为酶促反应最大速度；Km为米氏常数，是酶促反应达最大速度（Vm）一半时的底物(S)的浓度

　　米氏常数-定义 k1 k3

　　E+S〈——〉ES〈——〉E+P

　　k2 k4

　　其中，E为酶，S为底物，P为产物，k1，k2,k3,k4为反应速率

　　Km=（k2+k3）/k1

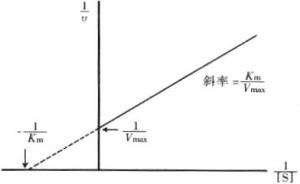米氏常数　　它的意义如下： 它的数值等于 酶促反应达到其最大速度Vm一半时的底物浓度〔S〕，图示以及公式推导。 它可以表示酶和底物之间的亲和能力，Km值越大，亲和能力越弱，反之亦然。 它可以确定一条 代谢途径中的限速步骤：代谢途径是指由一系列彼此密切相关的生化反应组成的代谢过程，前面一步反应的产物正好是后面一步反应的底物，例如， EMP途径。限速步骤就是一条代谢途径中反应最慢的那一步，Km值最大的那一步反应就是，该酶也叫这条途径的 关键酶。 它可以用来判断酶的最适底物，某些酶可以催化几种不同的生化反应，叫多功能酶，其中Km值最小的那个反应的底物就是酶的最适底物。 Km是一种酶的特征常数，只与酶的种类有关而与酶的浓度无关，与底物的浓度也无关，这一点与Vm是不同的，因此，我们可以通过Km值来鉴别酶的种类。但是它会随着反应条件（T、PH）的改变而改变。非竞争性抑制剂米氏常数不变，最大反应速度减小；反竞争性抑制剂米氏常数减小，最大反应速度减小。