- 指数不等式

指数不等式
中文名
指数不等式
所属学科
数学
基本介绍
指数里含有未知数的不等式叫作指数不等式。
形如![]() 或
或![]() (
(![]() ,且
,且![]() )的不等式叫作基本指数不等式或最简指数不等式。下列形式的每个不等式叫做初等指数不等式[1]:
)的不等式叫作基本指数不等式或最简指数不等式。下列形式的每个不等式叫做初等指数不等式[1]:
![]() 其中
其中![]() 。还有形如
。还有形如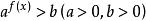 ,
,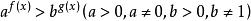 等的不等式也都是指数不等式。
等的不等式也都是指数不等式。
指数不等式的解法
①形如![]() 或
或![]() (
(![]() ,且
,且![]() )的不等式的解法
)的不等式的解法
理论依据是指数函数![]() 的单调性。
的单调性。
(1)当![]() 时,函数
时,函数![]() 是增函数;
是增函数;
(2)当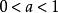 时,函数
时,函数![]() 是减函数。
是减函数。
下面我们研究不等式![]() 的解法:
的解法:
(1)当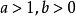 时,原不等式即为
时,原不等式即为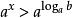 ,所以
,所以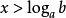 ;
;
(2)当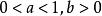 时,则有
时,则有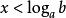 ;
;
(3)当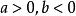 时,因
时,因![]() ,故
,故![]() [2]。
[2]。
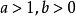 |
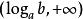 |
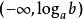 |
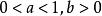 |
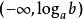 |
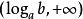 |
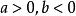 |
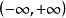 |
②形如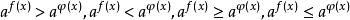 的解法
的解法
不等式: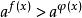 :
:
当![]() 时等价于不等式[1]
时等价于不等式[1]
![]()
当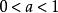 时等价于不等式
时等价于不等式
![]()
③形如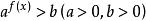 的解法
的解法
两边取常用对数:
![]()
④形如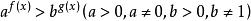
两边取常用对数: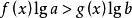 。
。
 收藏
收藏

相关百科
-
截断二进制指数退避算法
2025-09-27 09:00:22 查看详情 -
如何查询汽车价格定基指数 定基价格指数的概述
2025-09-27 09:00:22 查看详情 -
缺陷汽车产品召回管理规定 汽车召回规定解读:召回不等于退换
2025-09-27 09:00:22 查看详情


 求购
求购






