非定常湍流

湍流是流体的一种流动状态。当流速很小时，流体分层流动，互不混合，称为层流，也称为稳流或片流；逐渐增加流速，流体的流线开始出现波浪状的摆动，摆动的频率及振幅随流速的增加而增加，此种流况称为过渡流；当流速增加到很大时，流线不再清楚可辨，流场中有许多小漩涡，层流被破坏，相邻流层间不但有滑动，还有混合,形成湍流，又称为乱流、扰流或紊流。

在自然界中，我们常遇到流体作湍流，如江河急流、空气流动、烟囱排烟等都是湍流。

湍流是在大雷诺数下发生的，雷诺数较小时，黏滞力对流场的影响大于惯性力，流场中流速的扰动会因黏滞力而衰减，流体流动稳定，为层流；反之，若雷诺数较大时，惯性力对流场的影响大于黏滞力，流体流动较不稳定，流速的微小变化容易发展、增强，形成紊乱、不规则的湍流流场。

飞机颠簸与大气湍流密切相关，为预报飞机颠簸的出现，朱志愚分析了湍流的产生和发展，但没有考虑湍流作用在飞机上时飞机本身的反应，尤其是飞机的垂直过负荷，以及湍流作用下飞机的传递函数。普遍认为，有了较强的湍流就必然有较强的飞机颠簸。这种观点导致经常出现预报结果与事实不符的现象。事实上，有了较强的湍流，有时有较剧烈的飞机颠簸。而有时却是轻微的颠簸，甚至只是略有振颤。另一方面，在湍流不强时，有时却有一定强度的颠簸出现。因此，探明其原因对飞机颠簸的预报是有意义的。

在考虑各种高空天气条件下的飞行颠簸时，研究飞机对非定常湍流的反应是重要和必要的。在各种云状和急流区中飞行时飞机颠簸的许多特点，均可以用状态的非定常性来解释。

王永忠利用具有6个自由度的飞机的运动方程，研究了大气湍流对飞机垂直过负荷的影响，推导了飞机在湍流大气中过负荷的传递函数，并分析了飞机对非定常湍流的反应。研究表明，在亚音速下，飞机飞行速度增大，飞机颠簸增强；在同样的气象条件和大气湍流强度下，小型飞机的颠簸比大型机剧烈。

湍流是在连续介质范畴内流体的不规则运动，包含不同尺度的脉动。超声速湍流流动由于涉及激波、膨胀波、波系干扰、激波/湍流相互作用、激波/边界层相互作用、流动可压缩性，且超声速流场内常常也包含低速区，因此流动一般非常复杂。根据湍流脉动量计算方法的不同，湍流数值模拟方法分为三个层次：雷诺平均 NS 方程（RANS）模拟、大涡模拟（LES）和直接数值模拟（DNS）。

韩依宇通过高雷诺数圆柱绕流、超声速混合层流动、超声速圆柱底部流动验证了 DES 类方法对非定常湍流问题，尤其是超声速湍流问题的模拟能力。

非定常湍流圆柱绕流包含了分离剪切流，转挨，大尺度涡结构等复杂的流动现象，是用来考察DES类方法的经典算例。常见的计算条件有Re=3900和Re=140000两种。相对于Re=3900，实际工程应用问题的Re数往往远远高于这个值。因此可以采用Re=140000的圆柱绕流验证IDDES方法在高雷诺数湍流问题中的应用。

对于圆柱绕流问题，Re=140000时处于亚临界区，圆柱边界层内是层流，分离仍是层流分离，但已非常接近临界雷诺数。为避免考虑转挨的问题，一些文献的做法，是在整个计算区域内采用全湍流进行计算。这样计算结果应当与超临界雷诺数下的流动特征一致，因此与超临界雷诺数下的试验结果进行对比。

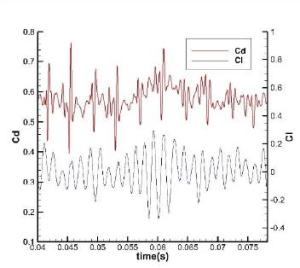升力和阻力系数随时间变化非定常计算过程中检测升力系数和阻力系数，得出升力系数和阻力系数随时间变化的曲线如图所示。由图可见，高雷诺数湍流非定常圆柱绕流有一定的周期性，但振幅和周期都随时间变化，这是因为尾迹区三维湍流流动除了主流外，还包含了复杂的湍流脉动和涡结构。

超声速混合层流动是典型的可压缩自由剪切湍流流动，大尺度涡在流动中起到重要作用，通过超声速混合层问题来检验 IDDES 方法对分离流流场涡结构的捕捉能力以及对平均量和脉动量统计平均值的预测能力。

控制方程分别采用二维和三维非定常 NS 方程，采用基于SST 模型的IDDES方法进行模拟。无粘通量计算采用重构-通量分裂法，重构采用基于特征变量的5阶 WENO 重构，通量分裂采用AUSMPW+格式，粘性项采用Gauss 定理计算，时间推进采用隐式双时间步法，时间步长为 5E-8s，子迭代步数为15 步，子迭代CFL 数为0.8。

分别采用二维网格和三维网格来计算此问题。对于二维计算，混合区长度取300mm，宽度取48mm，垂直方向的边界采用有滑移固壁边界（对称边界）条件。三维计算计算区域为二维计算区域在展向上延展 20mm，展向边界采用周期边界条件。二维计算的混合区网格量为600190 ，垂直壁面第一层网格法向长度取0.005mm。三维网格流向和法向网格分布与二维网格相同，在展向上均匀分布40个网格，混合区网格量为600x190x40。

超声速圆柱底部流动包含许多复杂的流动现象，如分离涡、激波，膨胀波等，适合用来对计算方法进行考核。

控制方程采用三维非定常 NS 方程，采用基于SST 模型的IDDES 方法进行模拟。无粘通量计算采用重构-通量分裂法，重构采用基于特征变量的5 阶WENO重构，通量分裂采用 AUSMPW+格式，粘性项采用Gauss定理计算，时间推进采用隐式双时间步法，时间步长为 4E-7s，子迭代步数为15 步，子迭代CFL 数为0.6。

计算区域底部上游取 8R，底部后取10R，径向的计算区域边界距圆柱对称轴距离为 4.15R。网格在近壁处进行加密，壁面第一层网格法向长度为0.005mm，总量为 800 万。