- 圆周卷积

圆周卷积
定义
x(t) 的周期延伸可以写成
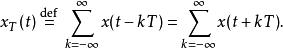 两个函数x(t) 与h(t) 的圆周卷积
两个函数x(t) 与h(t) 的圆周卷积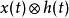 可用两种互相等价的方式来定义
可用两种互相等价的方式来定义
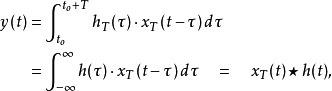 其中
其中![]() 表示原本的(线性)卷积。
表示原本的(线性)卷积。
类似的,对于离散信号(数列),可以定义周期N的圆周卷积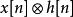 为
为
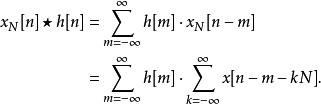
离散序列
类似地,对于离散序列和周期Ñ,我们可以写出循环卷积的功能ħ和X为:
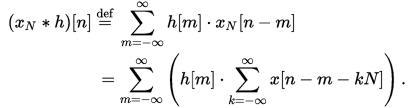
其中积分的内核变换是循环矩阵。[1]
算法
离散信号的圆周卷积可以经由圆周卷积定理使用快速傅立叶变换(FFT)而有效率的计算。因此,若原本的(线性)卷积能转换成圆周卷积来计算,会远比直接计算更快速。考虑到长度L 和长度 M 的有限长度离散信号,做卷积之后会成为长度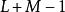 的信号,因此只要把两离散信号补上适当数目的零(zero-padding)成为N点信号,其中
的信号,因此只要把两离散信号补上适当数目的零(zero-padding)成为N点信号,其中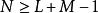 ,则它们的圆周卷积就与卷积相等。即可接着用N点 FFT 作计算。
,则它们的圆周卷积就与卷积相等。即可接着用N点 FFT 作计算。
用以上方法计算卷积时,若两个信号长度相差很多,则较短者须补上相当多的零,太不经济。而且在某些情况下,例如较短的h[n] 是一个 FIR 滤波器而较长的x[n] 是未知长度的输入(像语音)时,直接用以上方法要等所有的输入都收到后才能开始算输出信号,太不方便。这时可以把x[n] 分割成许多适当长度的区块(称为 block convolution),然后一段一段的处理。经过滤波后的段落再仔细的连接起来,借由输入或输出的重叠来处理区块连接的部份。这两种做法分别称为重叠-储存之卷积法和重叠-相加之卷积法。[2]
另见
- 离散希尔伯特变换
- 循环矩阵

相关百科


 求购
求购








