菲涅耳方程

当光从一种具有折射率为的介质向另一种具有折射率为的介质传播时，在两者的交界处（通常称作界面）可能会同时发生光的反射和折射。菲涅尔方程描述了不同光波分量被折射和反射的情况。也描述了波反射时的相变。

方程建立在反射面是平面，介质是光滑的，入射光是平面波，边际效应可被忽略的状态。

s 和 p 偏振

计算结果取决于入射光的偏振态。以下是两种情况（由于电场分量、磁场分量、光的传播方向有右手螺旋关系确定，所以仅讨论电场方向的偏振）

1. 偏振入射光的电场分量与入射光及反射光所形成的平面相互垂直。此时的入射光状态称为“s偏振态”，源于德语“senkrecht”。

   偏振入射光的电场分量与入射波及反射波所形成的平面相互平行。此时的入射光状态称为“p偏振态”，源于德语“parallel”。

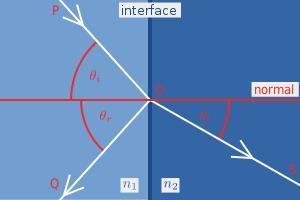菲涅耳方程中所用的变量

在右图中，入射光线PO到达两种介质交界面上的点O时，部分光线被反射，反射光为OQ，而另一部分被折射，折射光为OS。定义入射光线、反射光线和折射光线各自与法线形成的夹角分别为、和。

入射光与反射光由反射定律进行约束：

。

入射光与折射光由斯涅尔定律进行约束：

。

入射光的功率被界面反射的比例，我们称其为反射比；而将折射的比例称其为透射比。对反射比和透射比的计算需要用到电动力学中的电磁波传播理论，具体方法可参考玻恩的《光学原理：光的传播、干涉和衍射的电磁理论》以及杰克逊的《经典电动力学》。

反射比和透射比的具体形式还与入射光的偏振有关。如果入射光的电矢量垂直于右图所在平面（即s偏振），反射比为

其中是由斯涅尔定律从导出的，并可用三角恒等式化简。

如果入射光的电矢量位于右图所在平面内（即p偏振），反射比为

透射比无论在哪种情况下，都有。

如果入射光是无偏振的（含有等量的s偏振和p偏振），反射比是两者的算数平均值：。

反射和折射光波的振幅与入射光波振幅的比值（通常称为反射率和透射率）也可用类似的方程给出，这些方程也称作菲涅耳方程。根据不同的体系和符号习惯，它们可以有不同形式。反射率和透射率通常用小写的和表示。在某些体系中，它们满足条件：

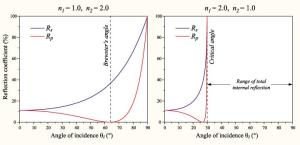
对于给定的折射率和且入射光为p偏振光时，当入射角为某一定值时为零，此时p偏振光被完全透射而无反射光出射。这个角度被称作布儒斯特角，对于空气或真空中的玻璃介质约为56°。注意这个定义只是对于两种折射率都为实数的介质才有意义，对于会吸光的物质，例如金属和半导体，折射率是一个复数，从而一般不为零。

当光从光密介质向光疏介质传播时（即时），存在一个临界的入射角，对于大于此入射角的入射光，此时入射光完全被界面反射。这种现象称作全内反射，临界角被称作全反射临界角，对于空气中的玻璃约为41°。

Fresnel2.png

当光线以近法线入射（）时，反射比和透射比分别为：

对于普通的玻璃，反射比大约为4%。注意窗户对光波的反射包括前面一层以及后面一层，因而少量光波会在两层之间来回振荡形成干涉。如忽略这种干涉效应，这两层合并后的反射比为（见下）。

需要指出的是这里所有的讨论都假设介质的磁导率都等于真空磁导率。对于大多数电介质而言这是近似正确的，但对其他类型的物质来说不正确，因而若考虑这一点则菲涅耳方程的形式会更加复杂。

当光在两层以上平行表面发生多重反射时，多列反射光波往往会互相发生干涉，从而有可能会使系统总的透射光和反射光振幅表达起来相当复杂，这通常是波长（或频率）的函数。一个例子是漂浮在水面上的油膜，在光照下会产生多种色彩；其他例子还包括法布里－珀罗干涉仪、透镜等光学仪器表面所用的能极大降低反射率的镀膜（增透膜），以及各种光学滤波器。对这些效应的定量计算仍然是基于菲涅耳方程的，但也要考虑额外产生的干涉所带来的影响，通常可以采用光学中的传递矩阵方法来计算这些问题。