- 曼戈尔特函数
曼戈尔特函数
定义
对每一个整数，我们定义
是
的牟比乌斯变换，而是
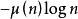的牟比乌斯变换。切比晓夫证明了若成立
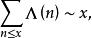则素数定理成立。
为了便于理解，我们将的值列于简表1中[1]。
 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
 |
 |
 |
|
 |
|
 |
|
 |
|
相关定理
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
|
|
|
|
|
|
|
|
|
曼戈尔特
对于曼戈尔特函数我们有如下定理．
定理1如果
，我们有
定理2设
为整数，且，则有
证明：对式(1)用麦比乌斯反演公式，因为对所有的正整数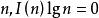
，因此可得
收藏
相关百科
求购