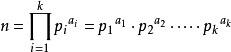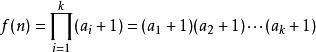约数个数定理

对于一个大于1正整数n可以分解质因数：

则n的正约数的个数就是。

其中a₁、a₂、a₃…a_k是p₁、p₂、p_3，…p_k的指数。

首先同上，n可以分解质因数：n=p1^a1×p2^a2×p3^a3*…*pk^ak,

由约数定义可知p1^a1的约数有:p1^0, p1^1, p1^2......p1^a1 ，共（a1+1）个;同理p2^a2的约数有（a2+1）个......pk^ak的约数有（ak+1）个。

故根据乘法原理：n的约数的个数就是(a1+1)(a2+1)(a3+1)…(ak+1)。

例题：正整数378000共有多少个正约数？

解：将378000分解质因数378000=2^4×3^3×5^3×7^1

由约数个数定理可知378000共有正约数(4+1)×(3+1)×(3+1)×(1+1)=160个。