- 幂指函数

幂指函数
定义
幂指函数指数和底数都是变量的函数,形如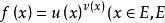 是数集)的函数称为幂指函数,其中 u,v 是 E 上的函数。
是数集)的函数称为幂指函数,其中 u,v 是 E 上的函数。
当不给出 u(x)与 v(x) 当具体形式时,总要求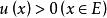 。因此,幂指函数可改写成由
。因此,幂指函数可改写成由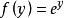 与
与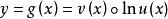 复合而成的函数 f(g(x)),从而当 u,v 连续时它连续,u,v 可微时它也可微。[2]
复合而成的函数 f(g(x)),从而当 u,v 连续时它连续,u,v 可微时它也可微。[2]
幂指函数既像幂函数,又像指数函数,二者的特点兼而有之。作为幂函数,其幂指数确定不变,而幂底数为自变量;相反地,指数函数却是底数确定不变,而指数为自变量。幂指函数就是幂底数和幂指数同时都为自变量的函数。这种函数的推广,就是广义幂指函数。
具体例子
最简单的幂指函数就是y=xx。说简单,其实并不简单,因为当你真正深入研究这种函数时,就会发现,在x<0时,函数图象存在“黑洞”——无数个间断点,如右图所示(用虚线表示)。
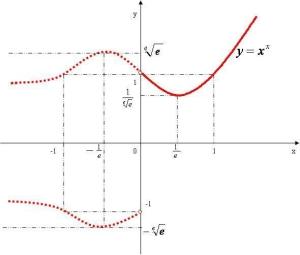 图1.最简单的幂指函数在x>0时,函数曲线是连续的,并且在x=1/e处取得最小值,约为0.6922,在区间(0,1/e]上单调递减,而在区间[1/e,+∞)上单调递增,并过(1,1)点。
图1.最简单的幂指函数在x>0时,函数曲线是连续的,并且在x=1/e处取得最小值,约为0.6922,在区间(0,1/e]上单调递减,而在区间[1/e,+∞)上单调递增,并过(1,1)点。
此外,从函数y=xx的图象可以清楚看出,0的0次方是不存在的。这就是为什么在初等代数中明文规定“任意非零实数的零次幂都等于1,零的任意非零非负次幂都等于零”的真正原因。
函数极限
本段中所有![]() 的记号,表示的是各种可能的趋向,即 *可以是a、a-0、a+0 、∞ 、-∞ 或+∞ 。
的记号,表示的是各种可能的趋向,即 *可以是a、a-0、a+0 、∞ 、-∞ 或+∞ 。
一般方法
利用恒等变形(即换底变形) 及复合函数
及复合函数![]() 求极限法则
求极限法则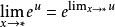 ,有
,有
![]()
待定型
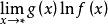 是两个函数乘积的极限,我们知道当且仅当
是两个函数乘积的极限,我们知道当且仅当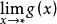 和
和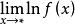 中有一个等于0,另一个为
中有一个等于0,另一个为![]() 时,极限
时,极限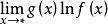 才是待定型。
才是待定型。
所以幂指函数极限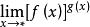 仅有三种待定型:
仅有三种待定型:![]() 型、
型、![]() 型、
型、![]() 型。
型。
肯定型
幂指函数的极限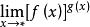 除了上述三种待定型外没有第四种待定型了。
除了上述三种待定型外没有第四种待定型了。
若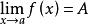 、
、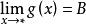 ,因为规定l了
,因为规定l了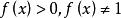 ,所以必有
,所以必有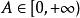 ,则
,则
(1)![]() ,(i)
,(i)![]() ,
,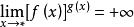 ;(ii)
;(ii)![]() ,
,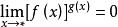 ;
;
(2)![]() ,
,![]() ,
,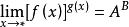 ;
;
(3)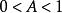 ,(i)
,(i)![]() 为
为![]() ,
,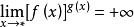 ;(ii)
;(ii)![]() 为为
为为![]() ,
,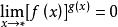 ;
;
(4)![]() ,(i)
,(i)![]() 为
为![]() ,
,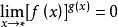 ;(ii)
;(ii)![]() 为为
为为![]() ,
,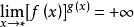 ;
;
(5)![]() 为+
为+![]() ,(i)
,(i)![]() 或
或![]() ,
,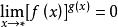 ;(ii)
;(ii)![]() 或
或![]() ,
,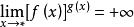 。
。
典例分析
(1)求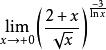 ,
,
解这个极限式“![]() 型”待定型,先求
型”待定型,先求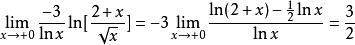 ,所以
,所以
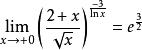 (2)求
(2)求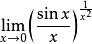 ,
,
解这个极限式是“![]() 型”待定型,先求
型”待定型,先求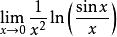 ,其中
,其中
![]()
利用等价无穷小关系公式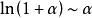 可作等价无穷小代换
可作等价无穷小代换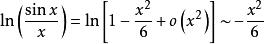 ,即可得
,即可得
![]() 所以
所以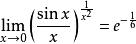 。
。
(3)求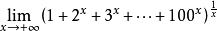
解这个极限式是“![]() 型”待定型,先求
型”待定型,先求![]() 待定型
待定型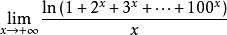 ,根据洛必达法则可得
,根据洛必达法则可得
![]()
![]()
所以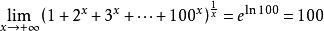 。
。
注本题也可以等价无穷大替代,或经过放大缩小 后再用夹逼准则计算。
后再用夹逼准则计算。
(4)求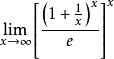 。
。
解这个极限式是“![]() 型”待定型,先计算
型”待定型,先计算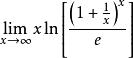 ,由于
,由于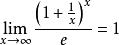 ,可知
,可知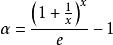 是
是![]() 时的无穷小量,利用等价无穷小关系
时的无穷小量,利用等价无穷小关系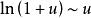 ,可得
,可得
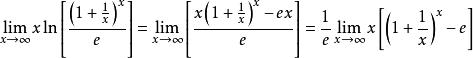
![]()
![]() 所以
所以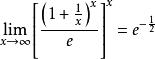 。
。
注 (1)这里“![]() 型”待定型中不能先把“底的极限1”先算出来,错成
型”待定型中不能先把“底的极限1”先算出来,错成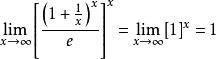 。
。
(2)解这种问题时除了使用洛必达法则外,经常会用到等价无穷小替代及换元方法。
求导方法
下面给出一般幂指函数的求导方法。为书写方便,把f(x)和g(x)分别用f和g代替,即![]()
指数求导法
由于幂指函数定义中f(x)>0,因此可以利用对数的性质将函数改写。 ,再对指数函数进行求导。
,再对指数函数进行求导。
![]()
对数求导法
这种方法是在两边取对数,再利用隐函数的求导法则求出y‘。
![]()
![]()
![]()
多元复合函数求导法
根据一元与多元函数复合的求导法则,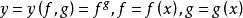 的导数为
的导数为
![]()

-
1641函数信号发生器
2025-11-02 16:26:42 查看详情


 求购
求购










