- 帕斯卡三角形

帕斯卡三角形
简介
杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623----1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合[2]。

概述
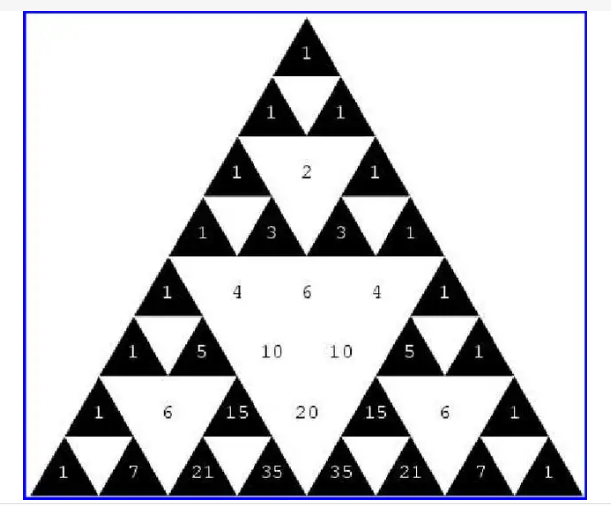 帕斯卡三角形(4)前提:每行端点与结尾的数为1.
帕斯卡三角形(4)前提:每行端点与结尾的数为1.
- 每个数等于它上方两数之和。
- 每行数字左右对称,由1开始逐渐变大。
- 第n行的数字有n项。
- 前n行共[(1+n)n]/2 个数。
- 第n行的m个数可表示为C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
- 第n行的第m个数和第n-m+1个数相等 ,为组合数性质之一。
- 每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一。即C(n+1,i)=C(n,i)+C(n,i-1)。
- (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
- 将第2n+1行第1个数,跟第2n+2行第3个数、第2n+3行第5个数……连成一线,这些数的和是第4n+1个斐波那契数;将第2n行第2个数(n>1),跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
- 将各行数字相排列,可得11的n-1(n为行数)次方:1=11^0; 11=11^1; 121=11^2……当n>5时会不符合这一条性质,此时应把第n行的最右面的数字"1"放在个位,然后把左面的一个数字的个位对齐到十位... ...,以此类推,把空位用“0”补齐,然后把所有的数加起来,得到的数正好是11的n-1次方。以n=11为例,第十一行的数为:1,10,45,120,210,252,210,120,45,10,1,结果为 25937424601=1110。
应用
性质5和性质7是杨辉三角的基本性质,是研究杨辉三角其他规律的基础。
与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即二项式定理。例如在杨辉三角中,第3行的三个数恰好对应着两数和的平方的展开式的每一项的系数(性质 8),第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数,即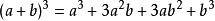 ,以此类推。
,以此类推。
又因为性质5:第n行的m个数可表示为C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。因此可得出二项式定理的公式为: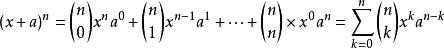
因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。求二项式展开式系数的问题,实际上是一种组合数的计算问题。用系数通项公式来计算,称为“式算”;用杨辉三角形来计算,称作“图算”[3]。
数在杨辉三角中的出现次数
由1开始,正整数在杨辉三角形出现的次数为∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... (OEIS:A003016)。最小而又大于1的数在贾宪三角形至少出现n次的数为2, 3, 6, 10, 120, 120, 3003, 3003, ... (OEIS:A062527)
除了1之外,所有正整数都出现有限次,只有2出现刚好一次,6,20,70等出现三次;出现两次和四次的数很多,还未能找到出现刚好五次的数。120,210,1540等出现刚好六次。(OEIS:A098565)
因为丢番图方程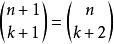 有无穷个解,所以出现至少六次的数有无穷个多。解为
有无穷个解,所以出现至少六次的数有无穷个多。解为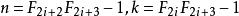 ,其中Fn表示第n个斐波那契数(F1=F2=1)。
,其中Fn表示第n个斐波那契数(F1=F2=1)。
3003是第一个出现八次的数。
历史沿革
 帕斯卡三角形北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算。
帕斯卡三角形北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算。
杨辉,字谦光,南宋时期杭州人。在他1261年所著的《详解九章算法》一书中,辑录了如上所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”。故此,杨辉三角又被称为“贾宪三角”。
元朝数学家朱世杰在《四元玉鉴》(1303年)扩充了“贾宪三角”成“古法七乘方图”。
意大利人称之为“塔塔利亚三角形”(Triangolo di Tartaglia)以纪念在16世纪发现一元三次方程解的塔塔利亚。
在欧洲直到1623年以后,法国数学家帕斯卡在13岁时发现了“帕斯卡三角”。
布莱士·帕斯卡的著作Traité du triangle arithmétique(1655年)介绍了这个三角形。帕斯卡搜集了几个关于它的结果,并以此解决一些概率论上的问题,影响面广泛,Pierre Raymond de Montmort(1708年)和亚伯拉罕·棣·美弗(1730年)都用帕斯卡来称呼这个三角形。
21世纪以来国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”(Chinese triangle)
历史上曾经独立绘制过这种图表的数学家有:
- 贾宪 中国北宋 11世纪 《释锁算术》
- 杨辉 中国南宋1261《详解九章算法》记载之功
- 朱世杰 中国元代 1299《四元玉鉴》级数求和公式
- 阿尔·卡西 阿拉伯 1427《算术的钥匙》
- 阿皮亚纳斯 德国 1527
- 米歇尔.斯蒂费尔 德国 1544《综合算术》二项式展开式系数
- 薛贝尔 法国 1545
- B·帕斯卡 法国 1654《论算术三角形》
其实,中国古代数学家在数学的许多重要领域中处于遥遥领先的地位。中国古代数学史曾经有自己光辉灿烂的篇章,而杨辉三角的发现就是十分精彩的一页。
在编程中实现
杨辉三角在编程实现中较为容易。最常见的算法便是用上一行递推计算;也有运用和组合的对应关系而使用阶乘计算的,然而后者速度较慢且阶乘容易溢出。编程的输出大多相类,此处并不过多添加截图。
C、C++、C#、Java 语言之间的语法也大多相类,因此这里也不会将每一种算法都在这些语言中各实现一遍。要在这些语言的版本间修改,实际上只需注意一些简单的语法和函数名称的改变,如 C 的 int yh[M][M] 应改写为 Java 的 int[][] yh = new int[M][M]、C# 的 int[,] yh=new int[M,M];C printf 应使用 Java 的 System.out.print、C# 的 Console.Write 、C++ 中更智能的 cout 来替换。
C++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
#include<iostream> #include<iomanip> using namespace std; int main() { const int n = 15; const int m = 2 * n-1; int arr[n + 1][m] = { 0 }; for (int i = 0; i < n; i++) { arr[i][n - i- 1] = 1; arr[i][n + i -1] = 1;
} for (int i = 2; i < n; i++) { for (int j = n - i + 1; j < n-2+i; j = j + 2) arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j + 1]; } int p; for (int i = 0; i < n; i++) { for (int j = 0; j < n - i - 1; j++) cout << " "; p = 1; for (int j = n - i - 1; p < i + 2; j = j + 2) { cout << setw(4) << arr[i][j] << " "; p = p + 1; } cout << endl; } return 0; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
#include <iostream> #include <cstring> #include <iomanip> using namespace std; int a[1000000]={0,1} , b[1000000];//这些随便改,想咋改咋改,用的是分类讨论! int main() { int n , i , j; cin >> n; for(i=2;i<=n+1;i++) { if(i%2==0) { for(j=1;j<=i;j++) b[j]=a[j]+a[j-1]; for(j=0;j<n-i+1;j++) cout << " "; for(j=1;j<i;j++) cout << setw(6) << setfill(' ') << a[j]; memset(a,0,sizeof(a)); } else { for(j=1;j<=i;j++) a[j]=b[j]+b[j-1]; for(j=0;j<n-i+1;j++) cout << " "; for(j=1;j<i;j++) cout << setw(6) << setfill(' ') << b[j]; memset(b,0,sizeof(b)); } cout << endl; } return 0; } |
Bash
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
#include<iostream> #include<iomanip> using namespace std; int main() { const int n = 15; const int m = 2 * n-1; int arr[n + 1][m] = { 0 }; for (int i = 0; i < n; i++) { arr[i][n - i- 1] = 1; arr[i][n + i -1] = 1;
} for (int i = 2; i < n; i++) { for (int j = n - i + 1; j < n-2+i; j = j + 2) arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j + 1]; } int p; for (int i = 0; i < n; i++) { for (int j = 0; j < n - i - 1; j++) cout << " "; p = 1; for (int j = n - i - 1; p < i + 2; j = j + 2) { cout << setw(4) << arr[i][j] << " "; p = p + 1; } cout << endl; } return 0; } |
C#
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
#include <iostream> #include <cstring> #include <iomanip> using namespace std; int a[1000000]={0,1} , b[1000000];//这些随便改,想咋改咋改,用的是分类讨论! int main() { int n , i , j; cin >> n; for(i=2;i<=n+1;i++) { if(i%2==0) { for(j=1;j<=i;j++) b[j]=a[j]+a[j-1]; for(j=0;j<n-i+1;j++) cout << " "; for(j=1;j<i;j++) cout << setw(6) << setfill(' ') << a[j]; memset(a,0,sizeof(a)); } else { for(j=1;j<=i;j++) a[j]=b[j]+b[j-1]; for(j=0;j<n-i+1;j++) cout << " "; for(j=1;j<i;j++) cout << setw(6) << setfill(' ') << b[j]; memset(b,0,sizeof(b)); } cout << endl; } return 0; } |
VisualBasic
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#! /bin/bash # 用法:./pasTrig [个数],若不指明个数为 5。 # 填充指定个数的空格 pad(){ for ((k=0;k<$1;k++)); do echo -n ' '; done; } # 层数和新旧层 lyrs=${1-5} prev[0]=1 curr[0]=1 # 接下来每行第一个始终为一,无需重复赋值 # 执行 pad $(((lyrs-1)*2)) echo 1 for ((i=2; i<=lyrs; i++)); do # 略过 1,已处理 pad $(((lyrs-i)*2)) # 填充空格,注意这里不会怎么顾及三位以上的数,即第 14 层开始会混乱 curr[i]=1 printf '%-4d' ${curr[0]} for ((j=1; j<i-1; j++)); do # 首尾极值已处理,略过 ((curr[j]=prev[j-1]+prev[j])) printf '%-4d' ${curr[j]} done printf '%-4d\n' ${curr[i]} # 最后一个和换行 # 搬家 prev=(${curr[*]}) done |
Bash 输出杨辉三角并使用 nl 表明行号
SQL
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#! /bin/bash # 用法:./pasTrig [个数],若不指明个数为 5。 # 填充指定个数的空格 pad(){ for ((k=0;k<$1;k++)); do echo -n ' '; done; } # 层数和新旧层 lyrs=${1-5} prev[0]=1 curr[0]=1 # 接下来每行第一个始终为一,无需重复赋值 # 执行 pad $(((lyrs-1)*2)) echo 1 for ((i=2; i<=lyrs; i++)); do # 略过 1,已处理 pad $(((lyrs-i)*2)) # 填充空格,注意这里不会怎么顾及三位以上的数,即第 14 层开始会混乱 curr[i]=1 printf '%-4d' ${curr[0]} for ((j=1; j<i-1; j++)); do # 首尾极值已处理,略过 ((curr[j]=prev[j-1]+prev[j])) printf '%-4d' ${curr[j]} done printf '%-4d\n' ${curr[i]} # 最后一个和换行 # 搬家 prev=(${curr[*]}) done |
易语言
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Program { public int yanghui(int value) { if(value<3) return 1; int[,]arry=new int[value,value]; Console.WriteLine("数组为:"); for(int i=0;i<value;i++) { string str=""; str=str.PadLeft(value-i); Console.Write(str); for(int j=0;j<=i;j++) { if(i==j||j==0) arry[i,j]=1; else arry[i,j]=arry[i-1,j-1]+arry[i-1,j]; Console.Write(arry[i,j]+""); } Console.WriteLine(); } }
static void Main(string[]args) { Program p=new Program(); Console.WriteLine("请输入数组值:"); if (p.yanghui(Convert.ToInt16(Console.ReadLine()))) Console.WriteLine("输入数值必须大于3"); Console.Readkey(); }
} |
以下的代码均用标准 C 语言写成,可以被包括 MSVC(含 VC6)、GCC 的多种 C 编译器编译。
这个算法使用只行列位置和左侧的数值算出数值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
/* yh-rt1.c - 时间和空间最优算法 */ #include <stdio.h> #include <stdlib.h> int main() { int s = 1, h; // 数值和高度 int i, j; // 循环计数 scanf("%d", &h); // 输入层数 printf("1\n"); // 输出第一个 1 for (i = 2; i <= h; s = 1, i++) // 行数 i 从 2 到层高 { printf("1 "); // 第一个 1 for (j = 1; j <= i - 2; j++) // 列位置 j 绕过第一个直接开始循环 //printf("%d ", (s = (i - j) / j * s)); printf("%d ", (s = (i - j) * s / j)); printf("1\n"); // 最后一个 1,换行 } getchar(); // 暂停等待 return 0; } |
默认求直角三角形,可通过注释的开关或使用编译器的 -D 定义开关调节等腰三角形和菱形输出。如果觉得复杂,可按照 define 使用的情况剔除因不符合 ifdef 条件从而未启用的代码之后阅读。
这个算法创建了一个二维数组,并且通过上一行的数值求当前行。在反过来再次打印时,这个程序会使用以前算好的值,从而节省了重复迭代的时间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
/* yh-2d.c - 二维数组迭代 */ #include<stdio.h> #define M 10 // 行数 // #define PYRAMID // 金字塔,会额外填充空格 // #define REVERSE // 反向再来一次,得到菱形 int main(void) { int a [M][M], i, j; // 二维数组和循环变量,a[行][列] for (i = 0; i<M; i++) // 每一行 { #ifdef PYRAMID for (j = 0;j <= M-i; j++) printf (" "); #endif // 填充结束 for (j = 0; j <= i; j++) // 赋值打印 printf("%4d", (a[i][j] = (i == j || j == 0) ? 1 : // 首尾置 1 a[i - 1][j] + a[i - 1][j - 1] )); // 使用上一行计算 printf("\n"); } #ifdef REVERSE for(i = M-2; i >= 0; i--) { #ifdef PYRAMID for (j = 0;j <= M - i; j++) printf(" "); #endif // 填充结束 for (j = 0;j <= i; j++) printf("%4d",a[i][j]); // 直接使用以前求得的值 printf("\n"); } #endif // 菱形结束 getchar(); // 暂停等待 } |
这一个使用大数组写成,风格更接近教科书上的 VC6 代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
/* yh-rt3.c - 较为暴力的大数组 */ #include <stdio.h> #include "string.h" int main() { int a[10000]; //容器,由n*(n+1)/2<=10000可知,n<=141 int b,CR,i; //b为当前行数,CR为要求显示的行数,i为循环数 printf("请输入要显示的行数(3~141):"); scanf("%d",&CR); YHSJ(CR); a[1]=a[2]=1; //前两行数值少且全为1,故直接输出 printf("%d\n",a[1]); printf("%d %d\n",a[1],a[2]); for(b=3;b<=CR;b++) //从第三行开始判断 { for(i=b;i>=2;i--) //从倒数第一个数开始加 a[i]=a[i]+a[i-1]; //杨辉三角的规律,没有值的数组默认为0 for(i=1;i<=b;i++) //显示循环 printf("%d ",a[i]); printf("\n"); // 换行 } return 0; } |
这个版本使用队列的方式输出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
#include <stdio.h> #include <stdlib.h> #define EMPTY 1 #define OFLOW 2 #define INVAL 3 #define MAX_Q 100 typedef int DataType; // 数据类型选择 typedef struct{ DataType elem[MAX_Q]; int front, rear; } LinkQ; // 队列及检查宏 #define InitQ(Q) LinkQ Q; Q.front=Q.rear=-1; #define _EQ(Q,e) Q.elem[(Q.rear=(Q.rear+1)%MAX_Q)]=e #define EnQ(Q,e) if((Q.rear+1)%MAX_Q==Q.front) Exit(OFLOW,"Overflow"); _EQ(Q,e) #define DeQ(Q,e) e=Q.elem[(Q.front=(Q.front+1)%MAX_Q)] #define Front(Q) Q.elem[(Q.front+1)%MAX_Q] // 退出 int Exit(int err, char msg[]) { puts(msg); exit(err); return err; } int main(void){ int n=1,i,j,k,t; InitQ(Q); printf("please enter a number:"); scanf("%d",&n); if (n<=0) { printf("ERROR!\n"); exit(INVAL); } for(i=0;i<n;i++) printf(" "); puts("1"); EnQ(Q,1); EnQ(Q,1); for(i=1;i<n;i++) { for(k=0;k<n-i;k++) printf(" "); EnQ(Q,1); for(j=0;j<i;j++){ DeQ(Q,t); printf("%3d ",t); EnQ(Q,t+Front(Q)); } EnQ(Q,1); DeQ(Q,t); printf("%d\n",t); } return 0; } |
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Program { public int yanghui(int value) { if(value<3) return 1; int[,]arry=new int[value,value]; Console.WriteLine("数组为:"); for(int i=0;i<value;i++) { string str=""; str=str.PadLeft(value-i); Console.Write(str); for(int j=0;j<=i;j++) { if(i==j||j==0) arry[i,j]=1; else arry[i,j]=arry[i-1,j-1]+arry[i-1,j]; Console.Write(arry[i,j]+""); } Console.WriteLine(); } }
static void Main(string[]args) { Program p=new Program(); Console.WriteLine("请输入数组值:"); if (p.yanghui(Convert.ToInt16(Console.ReadLine()))) Console.WriteLine("输入数值必须大于3"); Console.Readkey(); }
} |
PHP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
/* yh-rt1.c - 时间和空间最优算法 */ #include <stdio.h> #include <stdlib.h> int main() { int s = 1, h; // 数值和高度 int i, j; // 循环计数 scanf("%d", &h); // 输入层数 printf("1\n"); // 输出第一个 1 for (i = 2; i <= h; s = 1, i++) // 行数 i 从 2 到层高 { printf("1 "); // 第一个 1 for (j = 1; j <= i - 2; j++) // 列位置 j 绕过第一个直接开始循环 //printf("%d ", (s = (i - j) / j * s)); printf("%d ", (s = (i - j) * s / j)); printf("1\n"); // 最后一个 1,换行 } getchar(); // 暂停等待 return 0; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
/* yh-2d.c - 二维数组迭代 */ #include<stdio.h> #define M 10 // 行数 // #define PYRAMID // 金字塔,会额外填充空格 // #define REVERSE // 反向再来一次,得到菱形 int main(void) { int a [M][M], i, j; // 二维数组和循环变量,a[行][列] for (i = 0; i<M; i++) // 每一行 { #ifdef PYRAMID for (j = 0;j <= M-i; j++) printf (" "); #endif // 填充结束 for (j = 0; j <= i; j++) // 赋值打印 printf("%4d", (a[i][j] = (i == j || j == 0) ? 1 : // 首尾置 1 a[i - 1][j] + a[i - 1][j - 1] )); // 使用上一行计算 printf("\n"); } #ifdef REVERSE for(i = M-2; i >= 0; i--) { #ifdef PYRAMID for (j = 0;j <= M - i; j++) printf(" "); #endif // 填充结束 for (j = 0;j <= i; j++) printf("%4d",a[i][j]); // 直接使用以前求得的值 printf("\n"); } #endif // 菱形结束 getchar(); // 暂停等待 } |
词条图册
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
/* yh-rt3.c - 较为暴力的大数组 */ #include <stdio.h> #include "string.h" int main() { int a[10000]; //容器,由n*(n+1)/2<=10000可知,n<=141 int b,CR,i; //b为当前行数,CR为要求显示的行数,i为循环数 printf("请输入要显示的行数(3~141):"); scanf("%d",&CR); YHSJ(CR); a[1]=a[2]=1; //前两行数值少且全为1,故直接输出 printf("%d\n",a[1]); printf("%d %d\n",a[1],a[2]); for(b=3;b<=CR;b++) //从第三行开始判断 { for(i=b;i>=2;i--) //从倒数第一个数开始加 a[i]=a[i]+a[i-1]; //杨辉三角的规律,没有值的数组默认为0 for(i=1;i<=b;i++) //显示循环 printf("%d ",a[i]); printf("\n"); // 换行 } return 0; } |

-
第88届奥斯卡金像奖
2025-09-20 02:00:15 查看详情 -
鲍里斯·列昂尼多维奇·帕斯捷尔纳克
2025-09-20 02:00:15 查看详情 -
鲍利斯·列奥尼多维奇·帕斯捷尔纳克
2025-09-20 02:00:15 查看详情 -
新款凯迪拉克XT4申报图曝光 将使用碳纤维桶形座椅
2025-09-20 02:00:15 查看详情 -
新款凯迪拉克CT6申报图 将使用碳纤维桶形座椅
2025-09-20 02:00:15 查看详情


 求购
求购









