反对称关系

更准确地说，集合 X 上的二元关系 R 是反对称的，当且仅当对于X里的任意元素a, b，若a R-关系于 b 且 b R-关系于 a，则a=b。

用数学符号可写成：

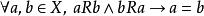
也可写作，

或等价地，

• 设X={1,2,3}，X上的两个二元关系为R₁={(1,1),(1,2),(2,3),(3,1)}, R₂={(1,2),(2,1),(2,3),(3,1)}。R₁是反对称的，R₂则不然。
• 实数集上的小于等于关系≤是反对称的，如果有两个实数x,y，x≤y且y≤x，则必有x=y。
• 设X为集合，则X的幂集P(X)上的子集关系⊆是反对称的：设A, B为P(X)的元素，即A, B是X的子集。若A⊆B 且B⊆A，则A=B。
• 实数的严格小于关系<是反对称的；实际上a<b且b<a是不可能的，因此严格不等的反对称性是一种空虚的真（vacuously true）。
• 任意集合上的空关系（empty relation），即关系为空集时。
• 整数上的整除关系|不是反对称的（因为1|-1，-1|1，但1≠-1）。如果限制在自然数范围内则是反对称的。
• 整数上的模n同余是对称的，但不是反对称的。

按照定义，偏序和全序都是反对称的。

注意，反对称关系不是对称关系（aRb → bRa）的反义。有些关系既是对称的又是反对称的，比如"等于"。有些关系既不是对称的也不是反对称的，比如上面说的整除例子。

非对称性（aRb∧~bRa）才算是对称关系的反义。事实上，非对称关系都符合反对称性（vacuously）。非对称关系亦即反对称的非自反关系。（）。

一个n元素集上共有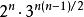个反对称关系。

自反的、对称的且可迁的关系称为等价关系，自反的且可迁的关系称为拟序关系，自反的、可迁的且反对称的关系称为序关系。