- 条件分布

条件分布
定义
二维随机向量![]() 中,
中,![]() 与
与![]() 的相互关系除了独立以外,还有相依关系,即随机变量的取值往往彼此是有影响的,这种关系用条件分布能更好地表达出来。
的相互关系除了独立以外,还有相依关系,即随机变量的取值往往彼此是有影响的,这种关系用条件分布能更好地表达出来。
对于二维随机向量![]() ,所谓随机变量X的条件分布,就是在
,所谓随机变量X的条件分布,就是在![]() 的条件下X的分布函数。比如,记X为人的体重,Y为人的身高,则X与Y一般有相依关系,现在如果限定Y=172(cm),在这个条件下体重X的分布显然与X的无条件分布有很大不同。
的条件下X的分布函数。比如,记X为人的体重,Y为人的身高,则X与Y一般有相依关系,现在如果限定Y=172(cm),在这个条件下体重X的分布显然与X的无条件分布有很大不同。
设给定二维随机向量![]() ,对任意
,对任意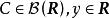 ,若
,若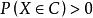 ,则
,则
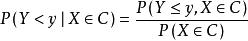 是一维分布函数,自然称它为条件
是一维分布函数,自然称它为条件![]() 下,
下,![]() 的条件分布函数。
的条件分布函数。
离散随机向量的条件分布
条件分布列
如果二维离散随机向量![]() 的联合分布列为
的联合分布列为
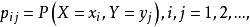 仿照条件概率的定义,我们很容易地给出离散随机向量的条件分布列。
仿照条件概率的定义,我们很容易地给出离散随机向量的条件分布列。
定义1对一切使得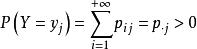 的
的![]() ,称
,称
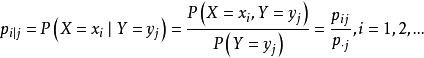 为在给定
为在给定![]() 条件下X的条件分布列。
条件下X的条件分布列。
同理,对一切使得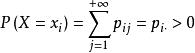 的
的![]() ,称
,称
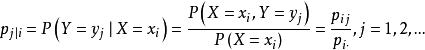 为在给定
为在给定![]() 条件下Y的条件分布列。
条件下Y的条件分布列。
条件分布函数
有了条件分布列,我们就可以定义离散随机向量的条件分布。
定义2在给定![]() 条件下X的条件分布函数为
条件下X的条件分布函数为
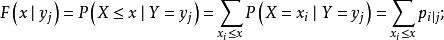 在给定
在给定![]() 条件下Y的条件分布函数为
条件下Y的条件分布函数为
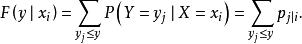
连续随机向量的条件分布
条件分布函数与条件密度函数
设![]() 为连续型随机向量,联合密度函数为
为连续型随机向量,联合密度函数为![]() ,边际分布函数分别为
,边际分布函数分别为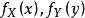 。
。
定义3对于一切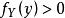 的
的![]() ,在给定
,在给定![]() 条件下,X的条件分布函数和条件密度函数分别为
条件下,X的条件分布函数和条件密度函数分别为
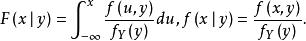 同理对于一切
同理对于一切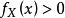 的x,在给定
的x,在给定![]() 条件下,Y的条件分布函数和条件密度函数分别为
条件下,Y的条件分布函数和条件密度函数分别为
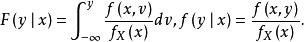
连续场合的全概率公式与贝叶斯公式
有了条件分布密度函数的概率,可以顺便给出连续随机变量场合的全概率公式和贝叶斯公式。
全概率公式
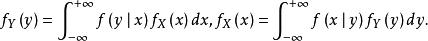
贝叶斯公式

相关百科
-
奥迪a6主动刹车系统如何开启(奥迪主动刹车系统的触发条件是什么)
2025-09-19 06:52:33 查看详情 -
比亚迪宋Plus 联手博世/采用分布式驱动
2025-09-19 06:52:33 查看详情 -
比亚迪海洋系轿车最新谍照 联手博世/采用分布式驱动
2025-09-19 06:52:33 查看详情 -
比亚迪秦PLUS 联手博世/采用分布式驱动
2025-09-19 06:52:33 查看详情 -
比亚迪海豹正式开启预售 联手博世/采用分布式驱动
2025-09-19 06:52:33 查看详情 -
比亚迪秦PLUS内饰设计图曝光 联手博世/采用分布式驱动
2025-09-19 06:52:33 查看详情 -
nanosox空气分布系统
2025-09-19 06:52:33 查看详情 -
纤维织物空气分布系统
2025-09-19 06:52:33 查看详情 -
低频信号发生器通用技术条件
2025-09-19 06:52:33 查看详情


 求购
求购



