- 取样定理
取样定理
主要内容
取样及取样定理的内容
连续信号的取样是由取样器(实际中为 A/D 转换器)来完成。 取样器就相当于一个电子开关,每隔 T 秒闭合一次,并对该电子开关的输出进行编码,得到原来连续信号![]() 在nT时刻的样本值
在nT时刻的样本值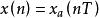 ,如下图所示:
,如下图所示:
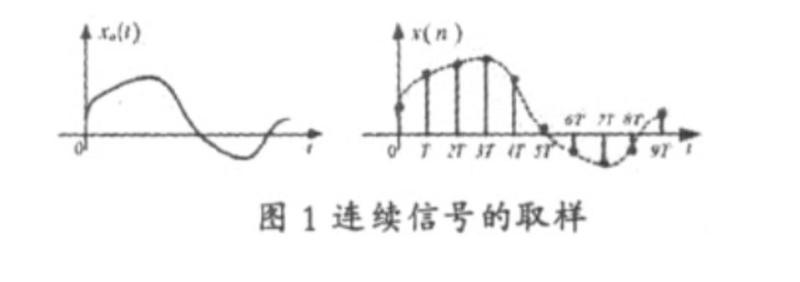
理想取样(周期单位冲激取样)
f(t)←→F(jω) (–ωm< ω<ωm)
s(t)←→S(jω)
fs(t)←→Fs (jω)
冲激取样信号的频谱
画fS(t)的频谱时,当ωS≥2ωm 时,其频谱不混叠,故能设法(如低通滤波器)从FS(j)中取出F(j),即从fS(t)中恢复原信号f(t); 否则发生混叠。
定理内容
奈奎斯特(Nyquist)和香农(Shannon)分别于 1928 年和1949 年 提 出 了 取样 定 理 ,取样 定 理 指出: 一个频谱在区间(-fh,fh)以外都为零的频带有限信号![]() ,可以唯一地由其在均匀间隔
,可以唯一地由其在均匀间隔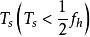 上的样值点
上的样值点![]() 确定[1]。
确定[1]。
取样定理论述了在一定条件下,一个连续信号完全可用离散样本值表示。利用这些样本值可恢复原信号[2]。
取样定理为连续信号与离散信号间的转换提供了理论依据。
地位
对于频谱有限函数,Shannon取样定理在函数逼近方面是一个重大的突破.取样定理来源于通信技术,但目前其应用远远超出此范围。工程技术上,如地球物理勘探、工业设计、图象处理等方面广泛应用到取样定理。
缺陷
收敛速度太慢、计算量大,从而误差较大之缺陷,还是不能适合高科技时代工程技术上的要求[3]。
发展
1.1986年,Natterer引入S空间中的速降函数,由此给出的取样定理大大加快了收敛速度,但由于速降函数不是初等函数,给计算带来了麻烦;
2.快速取样定理:对于![]() 中的任意b频谱有限函数f(x)成立:
中的任意b频谱有限函数f(x)成立:
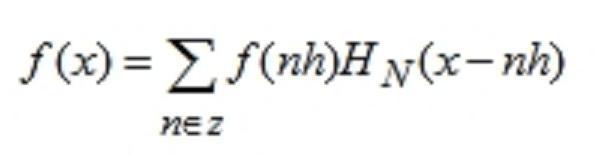
因为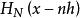 是初等函数,当|x|趋于无穷时,
是初等函数,当|x|趋于无穷时,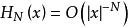 ,因此只需要选取适当的N,如选取N=3,4等值便可提高取样定理的收敛速度[3]。
,因此只需要选取适当的N,如选取N=3,4等值便可提高取样定理的收敛速度[3]。
工程应用
在实际应用过程中, 许多工程信号不是频带有限信号,即不满足取样定理,不能直接取样。 需要在取样之前加入抗混叠低通滤波器,去掉![]() 的高频成分,然后在进行取样。下图给出加抗混叠低通滤波器和不加抗混叠低通滤波器两种情况下,连续信号与取样信号的频谱图对比:
的高频成分,然后在进行取样。下图给出加抗混叠低通滤波器和不加抗混叠低通滤波器两种情况下,连续信号与取样信号的频谱图对比:
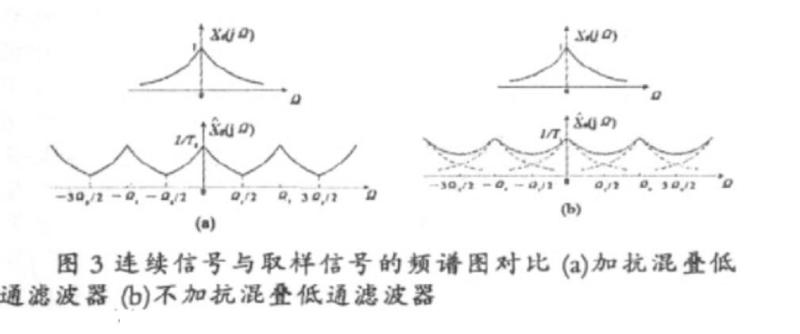
从中可以发现,加入抗混叠低通滤波器之后,频谱的混叠失真可以大大减小[1]。



 求购
求购






