- 积分中值定理

积分中值定理
积分第一中值定理内容
若函数![]() 在闭区间
在闭区间![]() 上连续,则在积分区间
上连续,则在积分区间![]() 上至少存在一个点
上至少存在一个点![]() ,使下式成立
,使下式成立
![]()
其中,a、b、![]() 满足:
满足: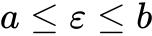 。
。
二重积分的中值定理
设f(x,y)在有界闭区域D上连续,![]() 是D的面积,则在D内至少存在一点
是D的面积,则在D内至少存在一点![]() ,使得:
,使得:
![]()
定理证明
![]() 在
在![]() 上连续,因为闭区间上连续函数必有最大最小值,不妨设最大值为
上连续,因为闭区间上连续函数必有最大最小值,不妨设最大值为![]() ,最小值为
,最小值为![]() ,最大值和最小值可相等。
,最大值和最小值可相等。
对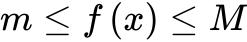 两边同时积分可得:
两边同时积分可得:
![]()
同除以![]() 从而得到:
从而得到:
![]()
由连续函数的介值定理可知,必定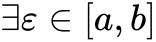 ,使得
,使得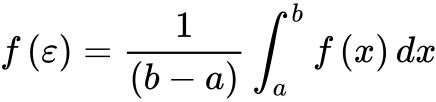 ,即:
,即:
![]()
命题得证。
积分第二中值定理
形式
![]() 在
在![]() 上Riemann可积,考虑下列两种情况:
上Riemann可积,考虑下列两种情况:
(1)![]() 在
在![]() 上单调递减且在
上单调递减且在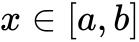 时,
时,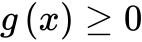 ,
,
那么存在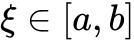 使得
使得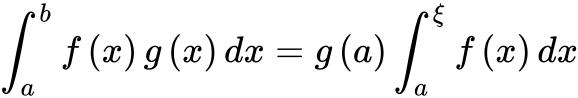 .
.
(2)![]() 在
在![]() 上单调递增且在
上单调递增且在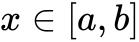 时,
时,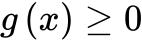 ,
,
那么存在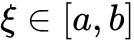 使得
使得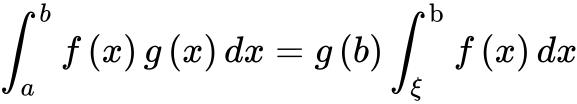 .[2]
.[2]
证明
只需证明第一种情况,第二种情况于此类似.设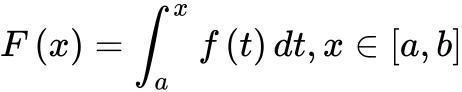 .
.![]() 是一个连续函数,故在
是一个连续函数,故在![]() 上有最小值
上有最小值![]() 和最大值
和最大值![]()
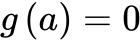 由单调性知道
由单调性知道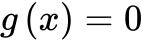 ,
,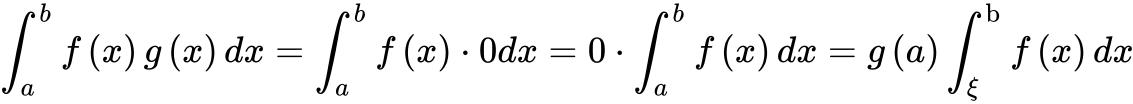 .
.
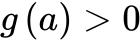 .因为
.因为![]() 在
在![]() 上是单调的,故可积,所以对任意
上是单调的,故可积,所以对任意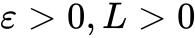 ,存在分割
,存在分割
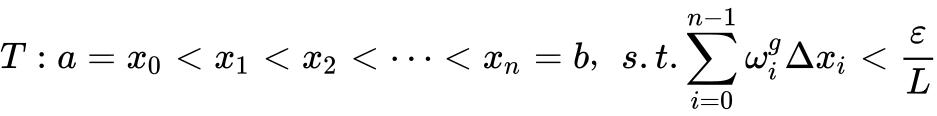 ,其中
,其中![]() 为
为![]() 在
在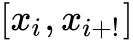 上的振幅.因
上的振幅.因![]() 在
在![]() 上黎曼可积,故有界,记为
上黎曼可积,故有界,记为![]() 则
则
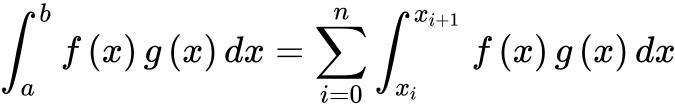
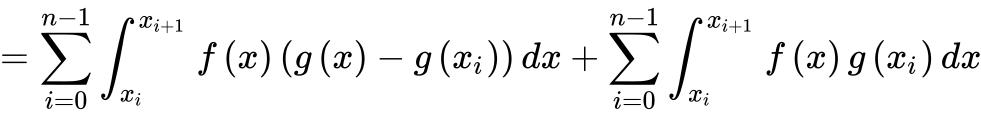
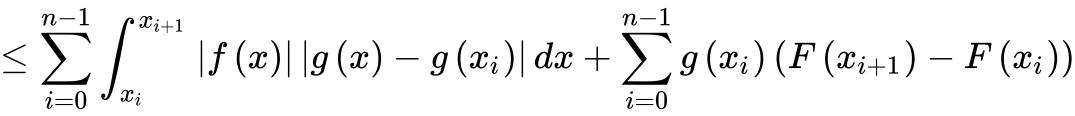
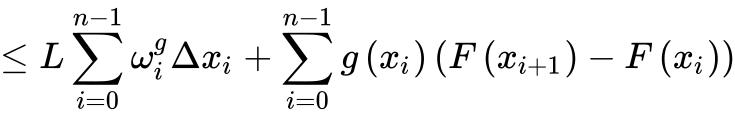
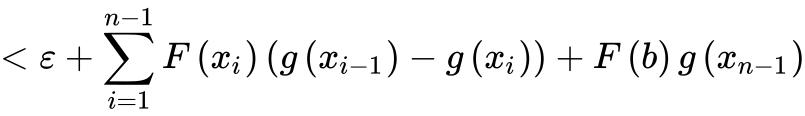
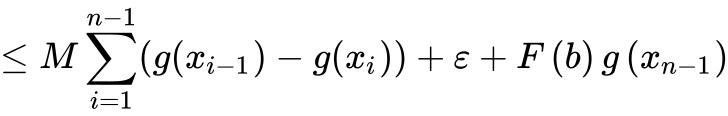
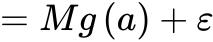
这里用到阿贝尔变换,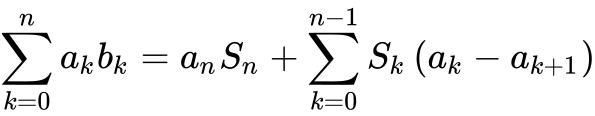
同理有原式
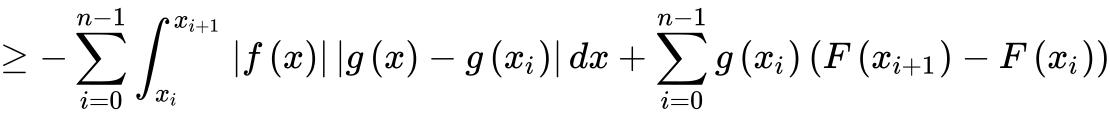
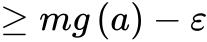 由上述证明知道
由上述证明知道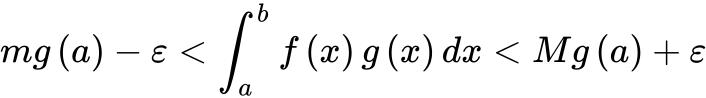
得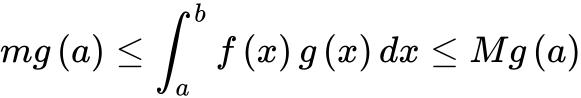 ,从而
,从而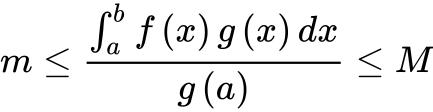
所以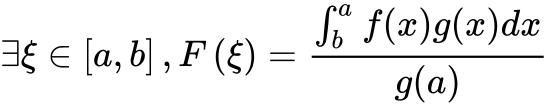 从而
从而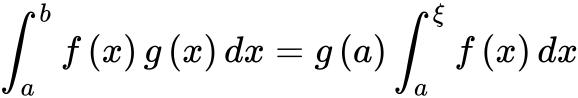 .[2]
.[2]
几何意义
这个定理的几何意义为:若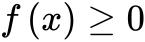 ,
,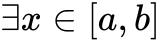 ,则由
,则由![]() 轴、
轴、![]() 、
、![]() 及曲线
及曲线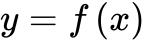 围成的曲边梯形的面积等于一个长为
围成的曲边梯形的面积等于一个长为![]() ,宽为
,宽为![]() 的矩形的面积。
的矩形的面积。
推广形式
第一定理
如果函数![]() 、
、![]() 在闭区间
在闭区间![]() 上连续,且
上连续,且![]() 在
在![]() 上不变号, 则在积分区间
上不变号, 则在积分区间![]() 上至少存在一个点
上至少存在一个点![]() ,使下式成立:
,使下式成立:
![]()
第二定理
一、如果函数![]() ,
,![]() 在闭区间
在闭区间![]() 上可积,且
上可积,且![]() 为单调函数,则在积分区间
为单调函数,则在积分区间![]() 上至少存在一个点
上至少存在一个点![]() ,,使下式成立:
,,使下式成立:
![]()
二、如果函数![]() 、
、![]() 在闭区间[a,b]上可积,
在闭区间[a,b]上可积,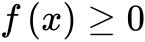 并且是单调递减函数,则在积分区间
并且是单调递减函数,则在积分区间![]() 上至少存在一个点
上至少存在一个点![]() , 使下式成立:
, 使下式成立:
![]()
三、如果函数![]() 、
、![]() 在闭区间
在闭区间![]() 上可积,且
上可积,且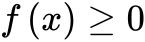 并是单调递增函数,则在积分区间
并是单调递增函数,则在积分区间![]() 上至少存在一个点
上至少存在一个点![]() ,使下式成立:
,使下式成立:
![]()
定理应用
积分中值定理在应用中所起到的重要作用是可以使积分号去掉,或者使复杂的被积函数化为相对简单的被积函数,从而使问题简化。因此,对于证明有关题设中含有某个函数积分的等式或不等式,或者要证的结论中含有定积分,或者所求的极限式中含有定积分时,一般应考虑使用积分中值定理, 去掉积分号,或者化简被积函数。
求极限
在函数极限的计算中, 如果含有定积分式, 常常可以运用定积分的相关知识, 比如积分中值定理等, 把积分号去掉。
 例题1
例题1
问题运用
 某些带积分式的函数, 常常会有要求判定某些性质的点的存在的问题, 有时运用积分中值定理能使问题迎刃而解。
某些带积分式的函数, 常常会有要求判定某些性质的点的存在的问题, 有时运用积分中值定理能使问题迎刃而解。
 例题2
例题2
运用估计
在大多数的积分式中, 能找到其被积函数的原函数再进行求值的积分简直是凤毛麟角, 当被积函数“积不出”或者原函数很复杂时, 可用各种方法来估计积分。对于乘积型的被积函数, 将变化缓慢的部分或积分困难的部分进行估计, 可积的部分积分之。积分中值定理和各种不等式就是其中常用的方法,
 例题3
例题3
不等式证明
积分不等式是指不等式中含有两个以上积分的不等式,当积分区间相同时,先合并同一积分区间上的不同积分,根据被积函数所满足的条件,灵灵活运用积分中值定理,以达到证明不等式成立的目的。
在证明定积分不等式时, 常常考虑运用积分中值定理, 以便去掉积分符号, 如果被积函数是两个函数之积时, 可考虑用积分第一或者第二中值定理。对于某些不等式的证明, 运用原积分中值定理只能得到“≥”的结论, 或者不等式根本不能得到证明。而运用改进了的积分中值定理之后, 则可以得到“![]() ”的结论, 或者成功的解决问题。
”的结论, 或者成功的解决问题。
 例题4
例题4

-
比例积分电动三通调节阀
2025-08-13 04:13:24 查看详情 -
加油卡怎么使用(邮政积分兑换加油卡怎么使用)
2025-08-13 04:13:24 查看详情 -
新款沃尔沃XC90上市 都是积分惹的祸
2025-08-13 04:13:24 查看详情


 求购
求购






