松弛法

松弛法是一种加速迭代方法，对于数值计算各种问题所采用的迭代法，均可起到加速收敛的作用。

此法产生于20世纪30年代，是基于变分思想的一种方法。其思想可描述如下： 假定把无重量的弹性弦拉成水平，然后在弦的一些点上加上负载，同时在每点上用与负载一样大的力向上拉，此时弦依然处于平衡状态，不产生弹性力，也没有位移。有规则地逐渐减小各点向上的拉力，位移与弹性力也随之产生，当各负载点向上的拉力减至零时，弦即处于松弛状态，最终得到各负载点的位移。拉力减小的过程，就是逐步逼近松弛状态的过程，松弛法由此得名。^[1]

一般地，我们可以使用松弛法解线性方程组。但松弛法的应用不限于此，对于微分方程及其他问题数值求解也是有用的。^[1]

此外还有超松弛法、群松弛法、逐次超松弛法等改进的松弛方法。^[1]

设线性代数方程组为。雅可比迭代和高斯-赛德尔迭代，在满足收敛的充分条件时，尽管迭代过程是收敛的，但还存在收敛速度的问题。如果迭代法的收敛速度很慢，则会使计算的工作量过大。这时就必须寻求加速的方法。下面介绍的线性加速收敛的方法称为松弛法。^[2]

以高斯-赛德尔迭代法为例。首先，由高斯-赛德尔迭代格式求得第次迭代值，即

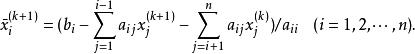然后计算这个第次迭代值与第次迭代值之差，即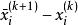。最后在第次迭代值的基础上，直接加上这个差的一个倍数作为实际的第次的迭代值，即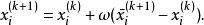

综合以上过程，可以得到如下的迭代格式：

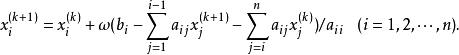式中，称为松弛因子。^[2]

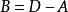设线性代数方程组为。记的对角线元素所成的对角矩阵为，，和分别为的下三角形和上三角形矩阵，则，故迭代格式也写为矩阵形式：

^[3]

迭代格式的矩阵形式可写成

的形式，其中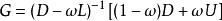称为迭代矩阵。则上述迭代过程收敛的充分必要条件为

其中，为的谱半径。

由此可得收敛的一个充分条件为

1）当时，称为超松弛法，此时加大了的比重；当时，称为亚松弛法或低松弛法；当时，就是一般的高斯-赛德尔迭代法。^[2]

2）若是对称正定矩阵，且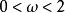，则SOR迭代法收敛。^[3]

3）若矩阵严格对角占优，或不可约对角占优，且，则SOR迭代法收敛。^[3]

3）在实际应用中，可以根据系数矩阵的性质及其反复计算的经验来选定合适的松弛因子，以加快收敛速度。^[2]