光学传递函数

生活中观察到的各类 物体，通过 光学仪器（如 照相机、 望远镜、 显微镜）和 光学系统看到、探测到的 图像和目标，通过 电荷耦合器件（CCD）、 数码相机和 计算机多媒体获得的 图形、图像，具有 颜色和 亮度两个重要的参数。限于考虑 二维的非相干 单色光平面图像，则图像的 光强分布就成为描绘、规定该图像的主要 参数。一幅单色光图像总是由缓慢变化的背景、粗大的物体和急剧变化的边缘、局部细节构成。 傅里叶光学中用 空间频率 来描述光强 空间变化的快慢程度，把图像中缓慢变化的成分看作图像的“ 低频”，而把急剧变化的成分看作图像的“ 高频”，单位是“1/毫米”，即每毫米中 光强变化的周期数。 空间频率等于0表明图像中没有光强变化（如一张白纸）。一幅图像中既有零频分量，又有非零频分量，后者包含了各种空间频率的 分量。零频分量代表平均光强，称图像的 直流分量；非零频分量又称图像的交流分量。光学成像系统对于各种空间频率成分的传递性能反映了该 系统的成像质量，可借助于系统对于不同空间频率余弦光栅的 传递特性来表征。

放置在系统输入 平面上、空间频率为 的 一维余弦光栅的 光强分布可表为：

( )=1+cos(2π )

通过系统后像的光强分布则为：

( )=1+ ( )·cos[2π + ( )]

式中 ( )为 调制度或反差度，代表交流分量的 幅度 ( )与 直流分量 的比。输入余弦 光栅的调制度为1，为满幅调制； ( )≤1，等号仅当 =0时才成立。 ( )表征系统对于空间频率为 的余弦信号的 调制度的衰减，称为 调制传递函数； ( )则表示余弦光栅亮条纹的位置向暗条纹位置的相对移动，称为 相位传递函数。复函数：

( )= ( )exp[i ( )]

称为 光学传递函数。调制传递函数是光学传递函数的模，归一化手续规定 (0)=1，说明任何 成像系统对于均匀一致的亮场（零频）总会响应。缓慢变化的背景和粗大物体通过系统形成的像比较清晰，系统的低频 调制传递函数比较高。 空间频率越高，调制传递函数越小，表明越细微的物体 光学系统的 分辨率越低，那些 ( )≈0的物体细节会在通过系统的像 强度分布中变得非常模糊乃至消失。调制传递函数 ( )全面反映了从低频到高频的分量的 传递特性，是评价系统成像质量的主要 指标。许多场合下 光学传递函数指的就是 调制传递函数。若干 成像系统串联时， 合成系统的光学传递函数是 子系统光学传递函数的乘积。

光学系统只有有限的孔径，空间频率过高时余弦光栅的 衍射光离轴角过大，不能进入系统，因此存在 截止频率（ 极限频率） 。对于非相干成像系统，

=1/ =2N.A./

式中 为成像系统的 数（ 焦距/ 孔径）， 为光波 波长，N.A.为 数值孔径。超过截止频率的图像细节将不能通过系统。为此，光学系统是低频滤波器。相同规格（如 数相同）的成像系统具有相同的截止频率。

评价大视场光学系统的成像质量时，不但要考虑低频、 中频和高频的 调制传递函数（MTF）的大小，还要全面评价对应于不同 视场的一系列传递函数曲线。轴外视场对于水平方向（子午方向）放置的余弦光栅和垂直方向（弧矢方向）放置光栅的调制传递函数并不相同，所以要同时考察子午MTF和弧矢MTF。一般说来，调制传递函数曲线整体越高，系统的成像质量越好。在某些应用中还需要考虑 相位传递函数。但在普通成像镜头生产线上，为了快速高效判别成像质量，可用几个甚至一个空间频率 的调制传递函数 ( )与 阈值的比较来作为镜头像质是否合格的 判据，产业部门这样的近似已经够用。 又称 特征频率，通常取 = /2。

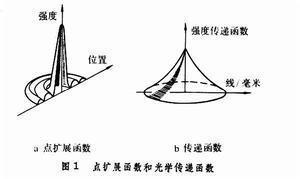为了得到 点光的像强度分布，必须考虑 衍射效应，才能对物和像之间关系有更全面理解。根 据 光的衍射理论可以研究 点光源至 透镜、至像平面光波的整个 传播过程，最后得出像平面上 强度分布是透镜 孔径函数的 夫琅和费衍射图样，称为 光学系统的强度脉冲响应，或 点扩展函数。由它可以确定光学系统的成像性质，因为任意复杂物体由无数点源组成，其像的 强度为物强度与点扩展函数的 卷积。图1a表示一个无 像差理想光学 成像系统的点扩展函数。

利用点扩展函数概念可对光学系统的 分辨率作出判据，例如对于两个点源组成的物，在像平面上的 强度分布是相应两 点扩展函数的 叠加。当两点源距离小于点扩展函数的半宽度即点扩展函数第一零点的半径时，两点源在像平面上不能分辨。

与研究电学系统相似，引入 傅里叶分析方法，考虑输入各种不同 空间频率的物函数，观察光学系统像面上输出情况，例如物是余弦形式的光栅。因光学系统是线性的，所以像强度分布也是余弦形式，但它的 振幅和 位相会受系统的影响。正弦光栅经光学系统成像后，比原物相比反衬度降低，最高强度降低，最低强度升高，设 T( )满足0≤ T( )≤1。另外还会产生 相移。原来亮线条的位置会向暗线条方向移动。 T( )是空间频率 的函数，改变 可测得 T( )随 变化曲线，反映系统对各空间频率的传递情况。对 T( )=1即零空间频率的 图像信息，在系统中传递不受损失；而对那些 T( )=0的图像频率成分，会在像 强度分布中消失。一般地， T( )是 复数，此时传递函数是实函数。

点扩展函数是一点光源经光学系统后所成的衍射斑分布的函数。它在 空域表征光学系统的特性， 传递函数在 频域表征系统的特性。实际上两者有简单关系，即点扩展函数的 傅里叶变换就是光学系统的传递函数。点扩展函数与透镜的 孔径函数有关， 传递函数也与孔径函数有关。事实上传递函数是孔径函数的 自相关函数。

一个光学系统质量的评价，早期采用“星点”法，即观察 点光源的像的 强度分布，实质上是把对点扩展函数形状的观察作为像质评价的判据。这种方法虽然直观，但带有主观性，不能作 定量评价。现在人们广泛用 传递函数作为像质评价的判据，使质量评价进入客观计量。