- 半加器

半加器
简介
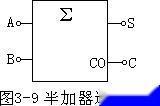
半加器是实现两个一位二进制数加法运算的器件。它具有两个输入端(被加数A和加数B)及输出端Y。[1]
是数据输入被加数A、加数B,数据输出S和数(半加和)、进位C0。
A和B是相加的两个数,S是半加和数,C是进位数。
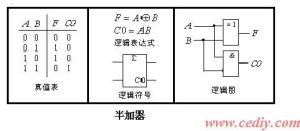
所谓半加就是不考虑进位的加法,它的真值表如下 (见表):[2]
| 被加数A | 加数B | 和数S | 进位数C |
| 0011 | 0101 | 0110 | 0001 |
表中:
![]()
![]()
分析
| 被加数A | 加数B | 和数S | 进位数C |
| 0011 | 0101 | 0110 | 0001 |
实现
由逻辑状态表可写出逻辑式,按组合数字电路的分析方法和步骤进行。
1.写出输出逻辑表达式
2.列出真值表
半加器的真值表见下表。表中两个输入是加数A0和B0,输出有一个是和S0,另一个是进位C0。
| 输入 | 输出 | ||
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
3.给出逻辑说明
半加器是实现两个一位二进制码相加的电路,因此只能用于两个二进制码最低位的相加。
 因为高位二进制码相加时,有可能出现低位的进位,因此两个加数相加时还要计算低位的进位,需要比半加器多进行一次相加运算。
因为高位二进制码相加时,有可能出现低位的进位,因此两个加数相加时还要计算低位的进位,需要比半加器多进行一次相加运算。
能计算低位进位的两个一位二进制码的相加电路,即为全加器。
输入和输出
| 输入 | 输出 | ||
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
与全加器区别
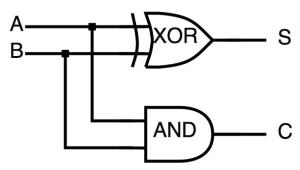 半加器的逻辑实现半加器不考虑低位向本位的进位,因此它不属于时序逻辑电路,有两个输入端和两个输出。
半加器的逻辑实现半加器不考虑低位向本位的进位,因此它不属于时序逻辑电路,有两个输入端和两个输出。
设加数(输入端)为A、B ;和为S ;向高位的进位为Ci+1
逻辑表达式: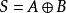 ;
;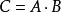 。
。



 求购
求购
