- 符号检验
符号检验
定义
广义
广义的符号检验是对连续变量π分位点Qπ进行的检验
狭义
狭义的符号检验则是仅针对中位数(或0.5分位点)M=Q0.5进行的检验。
规定
使用这种检验方法,对样本是否来自正态总体没有严格规定。它常用来检验两平均值的一致性。
若有![]() ,
,![]() ,K,
,K,![]() 和
和![]() ,
,![]() ,K,
,K,![]() 两组来自相同但未知分布的样本值,出现
两组来自相同但未知分布的样本值,出现![]() 或
或![]() 的几率是相同的,概率各为0.5,出现
的几率是相同的,概率各为0.5,出现![]() 或
或![]() 的次数C 是一个随机变量。
的次数C 是一个随机变量。
若将![]() =
=![]() 的情况不计,令出现
的情况不计,令出现![]() 的次数为
的次数为![]() ,出现
,出现![]() 的次数为
的次数为![]() ,令n =
,令n =![]() +
+![]() ,C= min(
,C= min(![]() ,
,![]() ) 。
) 。
如果由样本值得到的C 比符号检验临界值表中约定显著性水平a 的临界值Ca 还小,表明两平均值之间有系统误差。当n 很大时,C 遵从平均值为n / 2 、方差为n / 4 的正态分布。因此,可利用正态分布性质来检验两平均值。检验统计量是在约定显著性水平a = 0.05 , t 落入[-1.96,1.96]区间的概率为0.954,若由测量值计算的t 落入该区间之内,表明两平均值之间没有系统误差,否则,判为有系统误差。
步骤
假定检验的零假设为H0:Qπ=q0,而备择假设为H1:Qπ<q0、H1:Qπ>q0或H1:Qπ≠q0。记样本中小于q0的点数为S-,而大于q0的点数为S+,并且用小写的s+和s-分别代表S+和S-的实现值。记n=s++s-
在零假设H0:Qπ=q0下,S-应该服从二项分布Bin(n,π)。
由于n=s++s-,在所有样本点都不等于q0时,n就等于样本量;而如果有些样本点等于q0,那么这些样本点就不能参加推断(因为它们对判断分位点在哪里不起作用),应该把它们从样本中除去,这时,n就小于样本量。
对于连续变量,样本点等于q0的可能很小。
二项分布的P值
| 备选假设 | p值 | 使检验有意义的条件* |
| H1:Qπ>q0 | PH0(K≤ s-) | Qπ>q0 |
| H1:Qπ<q0 | 1-PH0(K≤ s--1) | Qπ<q0 |
| H1:Qπ≠q0 | 2min{PH0(K≤ s-),1-PH0(K≤ s--1)} |
说明
| 备选假设 | p值 | 使检验有意义的条件* |
| H1:Qπ>q0 | PH0(K≤ s-) | Qπ>q0 |
| H1:Qπ<q0 | 1-PH0(K≤ s--1) | Qπ<q0 |
| H1:Qπ≠q0 | 2min{PH0(K≤ s-),1-PH0(K≤ s--1)} |
符号检验法
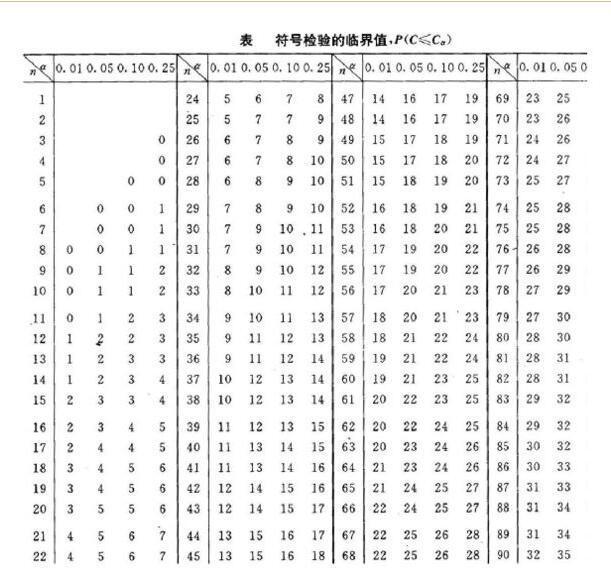
清点“+”、“-”、“0”各有几个,分别记为n+、n-、n0 进行显著性检验 查符号检验表(表中N=n+ +n− ):r=min(n+ ,n− ),查表,如r>表值,差异不显著,r≤表值,差异显著。[1]
应用
符号检验法是通过两个相关样本的每对数据之差的符号进行检验,从而比较两个样本的显著性。具体地讲,若两个样本差异不显著,正差值与负差值的个数应大致各占一半。[1]
符号检验与参数检验中相关样本显著性t检验相对应,当资料不满足参数检验条件时,可采用此法来检验两相关样本的差异显著性。
根据符号检验判断差异显著性时也要查表找出相应的临界值。但特别应注意的是在某一显著性水平下,实得的r值大于表中r的临界值时,表示差异不显著,这一点与参数检验时的统计量和临界值的判断结果不同。
基于排序集挑选抽样的分位数符号检验
基于非均等排序集抽样的符号检验
针对传统的符号统计量只能检验中位数的弊端,提出检验总体分位数的基于排序集挑选抽样的符号统计量。并通过分析挑选抽样与均衡抽样的Pinllan相对效率,具体给出不同分位数的最优抽样,弥补了排序集抽样在检验极端分位数上的不足。[2]

-
国家电线电缆质量监督检验中心
2025-09-16 03:01:48 查看详情 -
天津市医疗器械质量监督检验中心
2025-09-16 03:01:48 查看详情


 求购
求购





