- 独立性检验
独立性检验
定义
独立性检验是统计学的一种检验方式。与适合性检验同属于X2检验(即卡方检验,英文名:chi square test)它是根据次数资料判断两类因子彼此相关或相互独立的假设检验。
假设有两个分类变量X和Y,它们的值域分另为{x1, x2}和{y1, y2},其样本频数列联表为:
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
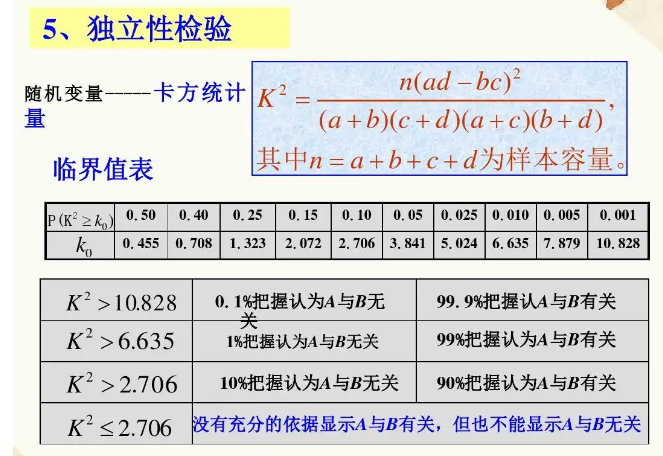
若要推断的论述为H1:“X与Y有关系”,可以利用独立性检验来考察两个变量是否有关系,并且能较精确地给出这种判断的可靠程度。具体的做法是,由表中的数据算出随机变量K^2的值(即K的平方)
K2= n (ad - bc)2/ [(a+b)(c+d)(a+c)(b+d)], 其中n=a+b+c+d为样本容量
K2的值越大,说明“X与Y有关系”成立的可能性越大。
当表中数据a,b,c,d都不小于5时,可以查阅下表来确定结论“X与Y有关系”的可信程度:
| P(K^2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K^2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
例如,当“X与Y有关系”的K2变量的值为6.109,根据表格,因为5.024≤6.109<6.635,所以“X与Y有关系”成立的概率为1-0.025=0.975,即97.5%。[1]
与列表相关联的概念
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
分类变量
| P(K^2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K^2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
列联表
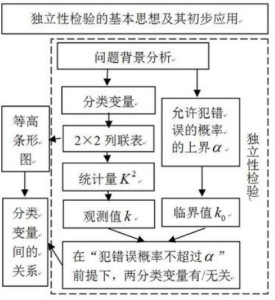
独立性检验的基本思想
 独立性检验(3)其不同“值”表示相应对象所属的不同类别的变量,分类变量的取值一定是离散的,而且不同的取值仅表示相应对象所属的类别,如性别变量只取男、女两个“值”,某商品的等级变量只取一级、二级、三级三个“值”,等等。分类变量的取“值”有时可用数字来表示,但这时的数字除了类别以外,没有其他的含义。如用“0”表示“男”,用“1”表示“女”。[1]
独立性检验(3)其不同“值”表示相应对象所属的不同类别的变量,分类变量的取值一定是离散的,而且不同的取值仅表示相应对象所属的类别,如性别变量只取男、女两个“值”,某商品的等级变量只取一级、二级、三级三个“值”,等等。分类变量的取“值”有时可用数字来表示,但这时的数字除了类别以外,没有其他的含义。如用“0”表示“男”,用“1”表示“女”。[1]
独立性检验的必要性
分类变量的统计汇总表(频数表)在独立性检验中,一般只研究两个分类变量,且每个分类变量只有两个可取的值;这时得到的列联表称为2×2列联表,如后面的案例中的关于患肺癌与否与吸烟与否的列联表。[1]
独立性检验的原理及步骤
独立性检验的案例展示
 独立性检验(4)独立性检验的学习目标:了解独立性检验的基本思想;
独立性检验(4)独立性检验的学习目标:了解独立性检验的基本思想;
独立性检验的学习重点:会对两个分类变量进行独立性检验。
即为什么不能只凭列联表中的数据和由其绘出的图形下结论,由列联表可以粗略地估计出两个变量(两类对象)是否有关(即粗略地进行独立性检验),但2×2列联表中的数据是样本数据,它只是总体的代表,具有随机性,故需要用独立性检验的方法确认所得结论在多大程度上适用于总体。关于这一点,在后面的案例中还要进一步说明。[2]
词条图册
独立性检验是一种假设检验(先假设,再推翻假设),它的原理及步骤与反证法类似。
反证法假设检验
要证明结论A想说明假设H1(两个分类变量,即两类对象有关)成立。在A不成立的前提下进行推理,在H1不成立,即H0(两类对象无关,即相互独立)成立的条件下进行推理,推出矛盾,意味着结论A成立,推出小概率事件(概率不超过α,α一般为0.001,0.01,0.05或0.1)发生,意味着H1成立的可能性很大(可能性为1-α),没有找到矛盾,意味着不能确定A成立,没有推出小概率事件发生,意味着不能确定H1成立。[2]

-
国家电线电缆质量监督检验中心
2025-11-03 08:20:03 查看详情 -
天津市医疗器械质量监督检验中心
2025-11-03 08:20:03 查看详情


 求购
求购





