- 紧集

紧集
定义
如果一个集合![]() 包含在某个球内,也即存在
包含在某个球内,也即存在![]() 和
和![]() 使得
使得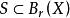 ,那么该集合是有界的(bounded)。
,那么该集合是有界的(bounded)。
有界的定义可以用某个固定的球心![]() 表述,因为如果一个集合包含在球
表述,因为如果一个集合包含在球![]() 中,那么它也包含在球
中,那么它也包含在球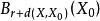 中。我们通常设定
中。我们通常设定![]() 来讨论有界性。
来讨论有界性。
如果![]() 是有界的闭集,那么S是紧集。[1]
是有界的闭集,那么S是紧集。[1]
相关概念
定义1设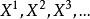 是
是![]() 中的一个点序列,设
中的一个点序列,设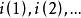 为一个正整数序列,并且
为一个正整数序列,并且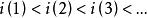 [这里将
[这里将![]() 写成
写成![]() 较为方便]。由
较为方便]。由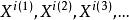 组成的序列称为
组成的序列称为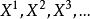 的子序列。如果对于所选择的
的子序列。如果对于所选择的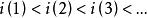 ,X“¨,
,X“¨,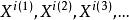 收敛,就说序列
收敛,就说序列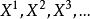 有一个收敛的子序列。
有一个收敛的子序列。
定义2假设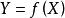 是一个函数,自变量为
是一个函数,自变量为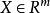 ,取值为
,取值为![]() 。设S为
。设S为![]() 的任意子集。则
的任意子集。则![]() 是指对
是指对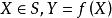 的集合。换言之
的集合。换言之
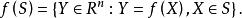
![]() 称为S(关于函数
称为S(关于函数![]() )的象(image)。[1]
)的象(image)。[1]
相关性质定理
定理1
![]() 是紧集,当且仅当每个序列
是紧集,当且仅当每个序列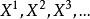 (其中
(其中![]() ,对
,对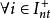 都有一个收敛于点
都有一个收敛于点![]() 的子序列。
的子序列。
定理2
如果![]() 是非空(
是非空(![]() )的紧集,那么S包含了一个最大数和一个最小数。
)的紧集,那么S包含了一个最大数和一个最小数。
证明:我们将证明集合S包含一个最大数。证明该集合包含一个最小数的方法是类似的。证明用到了有关实数集R的如下事实:如果一个非空的实数集有上界,那么它有最小上界(实数集S的上界是一个数b,对所有的![]() 有
有![]() )。也就是说,存在一个数,称为LUB或者S的上确界(sup),使得如果b是S的任意上界,有b≥sup(S)。假设
)。也就是说,存在一个数,称为LUB或者S的上确界(sup),使得如果b是S的任意上界,有b≥sup(S)。假设![]() 是非空(
是非空(![]() )的紧集。由于紧集是有界的,因而S有一个最小上界比如说
)的紧集。由于紧集是有界的,因而S有一个最小上界比如说![]() 。首先假设
。首先假设![]() ,那么
,那么![]() 是S中的最大数,否则就不是S的一个上界。接下来假设
是S中的最大数,否则就不是S的一个上界。接下来假设![]() 。我们将证明
。我们将证明![]() 是S中点序列的极限,并且,由于S是闭集,因而
是S中点序列的极限,并且,由于S是闭集,因而![]() 一定在S中。这与
一定在S中。这与![]() 的假设相矛盾。对每一个
的假设相矛盾。对每一个![]() ,存在一个
,存在一个![]() 使得
使得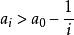 ,否则S将有一个小于
,否则S将有一个小于![]() 的上界。于是
的上界。于是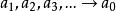 ,正如我们所要证明的。[1]
,正如我们所要证明的。[1]
定理3
设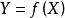 为从
为从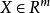 到
到![]() 的连续函数。如果
的连续函数。如果![]() 是紧集,那么
是紧集,那么![]() 也是紧集。
也是紧集。
证明:只需要证明,如果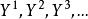 是
是![]() 中任意的点序列。那么存在一个收敛于
中任意的点序列。那么存在一个收敛于![]() 中某个点的子序列
中某个点的子序列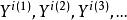 根据
根据![]() 的定义,在S中存在点
的定义,在S中存在点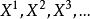 使得对任意的
使得对任意的![]() ,有
,有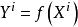 。由于S是紧集.因而存在
。由于S是紧集.因而存在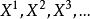 的一个子序列,称之为
的一个子序列,称之为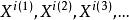 使得对
使得对![]() ,有
,有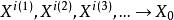 。又由于
。又由于![]() 是连续的,
是连续的,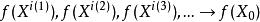 。但由于
。但由于![]() ,
,![]() 在
在![]() 中。因此
中。因此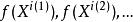 是
是![]() 的收敛于
的收敛于![]() 中一个点的子序列。[1]
中一个点的子序列。[1]
定理4
设S为![]() 的一个非空的紧子集,并设
的一个非空的紧子集,并设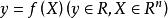 为一个连续函数。则S中存在一个
为一个连续函数。则S中存在一个![]() 和一个
和一个![]() ,使得
,使得
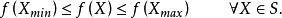 换言之,连续实值函数
换言之,连续实值函数![]() 在紧集S上既能取得极小值,也能取得极大值。
在紧集S上既能取得极小值,也能取得极大值。
证明:根据定理3,![]() 是紧集;根据定理2,由于
是紧集;根据定理2,由于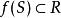 ,
,![]() 中存在
中存在![]() 和
和![]() ,使得
,使得
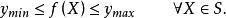
![]() 和
和![]() 是S中使
是S中使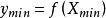 和
和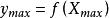 的点。[1]
的点。[1]



 求购
求购
