- 量子纠缠

量子纠缠
基本概念
假设一个零自旋中性π介子衰变成一个电子与一个正电子。这两个衰变产物各自朝着相反方向移动。电子移动到区域A,在那里的观察者“爱丽丝”会观测电子沿着某特定轴向的自旋;正电子移动到区域B,在那里的观察者“鲍勃”也会观测正电子沿着同样轴向的自旋。在测量之前,这两个纠缠粒子共同形成了零自旋的“纠缠态”![]() ,是两个直积态(product state)的叠加,以狄拉克标记表示为[3]
,是两个直积态(product state)的叠加,以狄拉克标记表示为[3]
![]() 其中,
其中,![]() 分别表示粒子的自旋为上旋或下旋。
分别表示粒子的自旋为上旋或下旋。
在圆括弧内的第一项表明,电子的自旋为上旋当且仅当正电子的自旋为下旋;第二项表明,电子的自旋为下旋当且仅当正电子的自旋为上旋。两种状况叠加在一起,每一种状况都有可能发生,不能确定到底哪种状况会发生,因此,电子与正电子纠缠在一起,形成纠缠态。假若不做测量,则无法知道这两个粒子中任何一个粒子的自旋,根据哥本哈根诠释,这性质并不存在。这单态的两个粒子相互反关联,对于两个粒子的自旋分别做测量,假若电子的自旋为上旋,则正电子的自旋为下旋,反之亦然;假若电子的自旋下旋,则正电子自旋为上旋,反之亦然。量子力学不能预测到底是哪一组数值,但是量子力学可以预言,获得任何一组数值的概率为50%。
粒子沿着不同轴向的自旋彼此之间是不相容可观察量,对于这些不相容可观察量作测量必定不能同时得到明确结果,这是量子力学的一个基础理论。在经典力学里,这基础理论毫无意义,理论而言,任何粒子性质都可以被测量至任意准确度。贝尔定理意味着一个事实,一个已被实验检试的事实,即对两个不相容可观察量做测量得到的结果不遵守贝尔不等式。因此,基础而言,量子纠缠是个非经典现象。[4]
不确定性原理的维持必须倚赖量子纠缠机制。例如,设想先前的一个零自旋中性π介子衰变案例,两个衰变产物各自朝着相反方向移动,分别测量电子的位置与正电子的动量,假若量子纠缠机制不存在,则可借着守恒定律预测两个粒子各自的位置与动量,这违反了不确定性原理。由于量子纠缠机制,粒子的位置与动量遵守不确定性原理。
从以相对论性速度移动的两个参考系分别测量两个纠缠粒子的物理性质,尽管在每一个参考系,测量两个粒子的时间顺序不同,获得的实验数据仍旧违反贝尔不等式,仍旧能够可靠地复制出两个纠缠粒子的量子关联。
研究历史
 量子纠缠(4)1935年,在普林斯顿高等研究院,爱因斯坦、博士后罗森、研究员波多尔斯基合作完成论文《物理实在的量子力学描述能否被认为是完备的?》,并且将这篇论文发表于5月份的《物理评论》。这是最早探讨量子力学理论对于强关联系统所做的反直觉预测的一篇论文。在这篇论文里,他们详细表述EPR佯谬,试图借着一个思想实验来论述量子力学的不完备性质。他们并没有更进一步研究量子纠缠的特性。[5]
量子纠缠(4)1935年,在普林斯顿高等研究院,爱因斯坦、博士后罗森、研究员波多尔斯基合作完成论文《物理实在的量子力学描述能否被认为是完备的?》,并且将这篇论文发表于5月份的《物理评论》。这是最早探讨量子力学理论对于强关联系统所做的反直觉预测的一篇论文。在这篇论文里,他们详细表述EPR佯谬,试图借着一个思想实验来论述量子力学的不完备性质。他们并没有更进一步研究量子纠缠的特性。[5]
薛定谔阅读完毕EPR论文之后,有很多心得感想,他用德文写了一封信给爱因斯坦,在这封信里,他最先使用了术语Verschränkung(他自己将之翻译为“纠缠”),这是为了要形容在EPR思想实验里,两个暂时耦合的粒子,不再耦合之后彼此之间仍旧维持的关联。不久之后,薛定谔发表了一篇重要论文,对于“量子纠缠”这术语给予定义,并且研究探索相关概念。薛定谔体会到这概念的重要性,他表明,量子纠缠不只是量子力学的某个很有意思的性质,而是量子力学的特征性质;量子纠缠在量子力学与经典思路之间做了一个完全切割。如同爱因斯坦一样,薛定谔对于量子纠缠的概念并不满意,因为量子纠缠似乎违反在相对论中对于信息传递所设定的速度极限。后来,爱因斯坦更讥讽量子纠缠为鬼魅般的超距作用。
EPR论文很显然地引起了众多物理学者的兴趣,启发他们探讨量子力学的基础理论。但是除了这方面以外,物理学者认为这论题与现代量子力学并没有什么牵扯,在之后很长一段时间,物理学术界并没有特别重视这论题,也没有发现EPR论文可能有什么重大瑕疵。EPR论文试图建立定域性隐变量理论来替代量子力学理论。1964年,约翰·贝尔提出论文表明,对于EPR思想实验,量子力学的预测明显地不同于定域性隐变量理论。概略而言,假若测量两个粒子分别沿着不同轴向的自旋,则量子力学得到的统计关联性结果比定域性隐变量理论要强很多,贝尔不等式定性地给出这差别,做实验应该可以侦测出这差别。因此,物理学者做了很多检试贝尔不等式的实验。
1972年,约翰·克劳泽与史达特·弗利曼(Stuart Freedman)首先完成这种检试实验。1982年,阿兰·阿斯佩的博士论文是以这种检试实验为题目。他们得到的实验结果符合量子力学的预测,不符合定域性隐变量理论的预测,因此证实定域性隐变量理论不成立。但是,每一个相关实验都存在有漏洞,这造成了实验的正确性遭到质疑,在作总结之前,还需要完成更多精确的实验。
这些年来,众多研究结果促成了应用这些超强关联来传递信息的可能性,从而导致了量子密码学的成功发展,最著名的有查理斯·贝内特(Charles Bennett)与吉勒·布拉萨(Gilles Brassard)发明的BB84协议、阿图尔·艾克特(Artur Eckert)发明的E91协议。
2017年6月16日,量子科学实验卫星墨子号首先成功实现,两个量子纠缠光子被分发到相距超过1200公里的距离后,仍可继续保持其量子纠缠的状态。
2018年4月25日,芬兰阿尔托大学教授麦卡﹒习岚帕(Mika Sillanpää)领导的实验团队成功地量子纠缠了两个独自震动的鼓膜。每个鼓膜的宽度只有15微米,约为头发的宽度,是由10个金属铝原子制成。通过超导微波电路,在接近绝对温度(-273.15摄氏度)下,两个鼓膜持续进行了约30分钟的互动。这实验演示出巨观的量子纠缠。
2019年12月28日,英国和丹麦科学家称,他们首次利用被称作“量子纠缠”的物理现象,实现了信息在两个计算机芯片之间的“瞬间传输”,此举可能催生更安全的“量子网络”。这项研究的论文发表在《自然物理学》期刊上。[6]
2020年7月,据国外媒体报道,在近期的一项研究中,物理学家创造了一项新的记录,他们将15万亿个原子组成的“热云”通过量子纠缠的方式关联起来。[7]
数学表述
假设一个复合系统是由两个子系统A、B所组成,这两个子系统A、B的希尔伯特空间分别为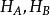 ,则复合系统的希尔伯特空间
,则复合系统的希尔伯特空间![]() 为张量积
为张量积
![]()
设定子系统A、B的量子态分别为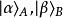 ,假若复合系统的量子态
,假若复合系统的量子态![]() 不能写为张量积
不能写为张量积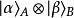 ,则称这复合系统为子系统A、B的纠缠系统,两个子系统A、B相互纠缠。
,则称这复合系统为子系统A、B的纠缠系统,两个子系统A、B相互纠缠。
纠缠度量
 量子纠缠(3)量子纠缠与量子系统失序现象、量子信息丧失程度密切相关。量子纠缠越大,则子系统越失序,量子信息丧失越多;反之,量子纠缠越小,子系统越有序,量子信息丧失越少。因此,冯诺伊曼熵可以用来定量地描述量子纠缠,另外,还有其它种度量也可以定量地描述量子纠缠。对于两体复合系统,这些纠缠度量较常遵守的几个规则为[3]:
量子纠缠(3)量子纠缠与量子系统失序现象、量子信息丧失程度密切相关。量子纠缠越大,则子系统越失序,量子信息丧失越多;反之,量子纠缠越小,子系统越有序,量子信息丧失越少。因此,冯诺伊曼熵可以用来定量地描述量子纠缠,另外,还有其它种度量也可以定量地描述量子纠缠。对于两体复合系统,这些纠缠度量较常遵守的几个规则为[3]:
- 纠缠度量必须映射从密度算符至正实数。
- 假若整个复合系统不处于纠缠态,则纠缠度量必须为零。
- 对于纯态复合系统,纠缠度量必需约化为冯诺伊曼熵。
- 对于命定性的定域运算与经典通讯(local operation and classical communication)变换,纠缠度量不会增加。
对于两体纯态,只有冯诺伊曼熵能够量度量子纠缠,因为只有它能够满足某些量度量子纠缠必须遵守的判据。对于混合态,使用冯诺伊曼熵并不是能够量度量子纠缠的独有方法。
不可分性
假设一个量子系统是由几个处于量子纠缠的子系统组成,而整体系统所具有的某种物理性质,子系统不能私自具有,这时,不能够对子系统给定这种物理性质,只能对整体系统给定这种物理性质,它具有“不可分性”。不可分性不一定与空间有关,处于同一区域的几个物理系统,只要彼此之间没有任何纠缠,则它们各自可拥有自己的物理性质。物理学者艾雪·佩雷斯(Asher Peres)给出不可分性的数学定义式,可以计算出整体系统到底具有可分性还是不可分性。假设整体系统具有不可分性,并且这不可分性与空间无关,则可将它的几个子系统分离至两个相隔遥远的区域,这动作凸显出不可分性与定域性的不同──虽然几个子系统分别处于两个相隔遥远的区域,仍旧不可将它们个别处理。在EPR佯谬里,由于两个粒子分别处于两个相隔遥远的区域,整体系统被认为具有可分性,但因量子纠缠,整体系统实际具有不可分性,整体系统所具有明确的自旋z分量,两个粒子各自都不具有。
案例解析
以两颗向相反方向移动但速率相同的电子为例,即使一颗行至太阳边,一颗行至冥王星边,在如此遥远的距离下,它们仍保有关联性(correlation);亦即当其中一颗被操作(例如量子测量)而状态发生变化,另一颗也会即时发生相应的状态变化。如此现象导致了鬼魅似的超距作用之猜疑,仿佛两颗电子拥有超光速的秘密通信一般,似与狭义相对论中所谓的定域性原理相违背。这也是当初阿尔伯特·爱因斯坦与同僚玻理斯·波多斯基、纳森·罗森于1935年提出的EPR佯谬来质疑量子力学完备性的理由。
具有量子纠缠的两颗电子——电子1和电子2,其自旋性质之纠缠态可以下面式子为例:
![]() 无法写成
无法写成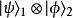 ,即两个量子态的张量积。 下标1和2表示这是电子1和电子2的量子态,采取
,即两个量子态的张量积。 下标1和2表示这是电子1和电子2的量子态,采取![]() 表示自旋的z方向分量向上,
表示自旋的z方向分量向上,![]() 表示自旋的z方向分量向下。
表示自旋的z方向分量向下。
太阳边的科学家决定对电子1做投影式量子测量,其测到的随机性结果不是![]() 就是
就是![]() 。当其测量结果显示为状态
。当其测量结果显示为状态![]() ,则冥王星的科学家在此之后,或很近、或较远的时间点对电子2做测量,必定会测到
,则冥王星的科学家在此之后,或很近、或较远的时间点对电子2做测量,必定会测到![]() 状态。因为投影式量子测量已经将原先量子态
状态。因为投影式量子测量已经将原先量子态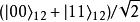 选择性地坍缩到
选择性地坍缩到![]() ,也可写成
,也可写成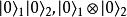 。这样,可以从电子1状态是
。这样,可以从电子1状态是![]() 知道选择到
知道选择到![]() 这一边。
这一边。
注意到: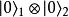 已经是两个成员系统各自量子态的张量积,所以测量后状态已非纠缠态。
已经是两个成员系统各自量子态的张量积,所以测量后状态已非纠缠态。
主要应用
量子纠缠是一种物理资源,如同时间、能量、动量等等,能够萃取与转换。应用量子纠缠的机制于量子信息学,很多平常不可行的事务都可以达成:
- 量子密钥分发能够使通信双方共同拥有一个随机、安全的密钥,来加密和解密信息,从而保证通信安全。在量子密钥分发机制里,给定两个处于量子纠缠的粒子,假设通信双方各自接受到其中一个粒子,由于测量其中任意一个粒子会摧毁这对粒子的量子纠缠,任何窃听动作都会被通信双方侦测发觉。
- 密集编码(superdense coding)应用量子纠缠机制来传送信息,每两个经典位元的信息,只需要用到一个量子位元,这科技可以使传送效率加倍。
- 量子隐形传态应用先前发送点与接收点分享的两个量子纠缠子系统与一些经典通讯技术来传送量子态或量子信息(编码为量子态)从发送点至相隔遥远距离的接收点。
- 量子算法(quantum algorithm)的速度时常会胜过对应的经典算法很多。但是,在量子算法里,量子纠缠所扮演的角色,物理学者尚未达成共识。有些物理学者认为,量子纠缠对于量子算法的快速运算贡献很大,但是,只倚赖量子纠缠并无法达成快速运算。
- 在量子计算机体系结构里,量子纠缠扮演了很重要的角色。例如,在一次性量子计算机(one-way quantum computer)的方法里,必须先制备出一个多体纠缠态,通常是图形态(graph state)或簇态(cluster state),然后借着一系列的测量来计算出结果。

-
蚁人与黄蜂女:量子狂潮
2025-09-19 06:18:38 查看详情


 求购
求购









