复流形

单复变函数论中的全纯函数的反函数经常出现多值情形，因此定义域便从复平面扩产到黎曼曲面，使得在黎曼曲面上这个全纯函数的反函数单值化。无支点的黎曼曲面的推广，就是复流形。

定义如下：设 M 为具有可数基的仿紧拓扑空间，在 M 上有开覆盖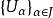，使得对每个开子集，存在到 n 维复欧几里得空间中开集上的同胚。

因此对开子集中每一点 p，存在局部坐标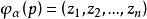。称为标架，称为坐标系。当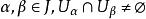，则开子集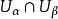中任一点 p 有两种坐标

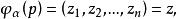
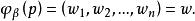由于和为同胚，于是有局部坐标 z 和 w 之间的一一对应关系：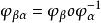

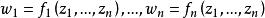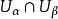这是（）到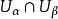（）上的映射，如果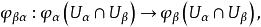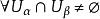是全纯同构映射，则拓扑空间 M 称为 n 维复流形。

注意，n 维复流形是一类特殊的 2n 维实流形，即具有复结构 J 的 2n 维实流形。上面提到黎曼曲面是由全纯函数的反函数单值化产生的。而在多复变情形，从解析开拓的角度，可以看出复欧几里得空间中的域上的全纯函数，在作解析开拓后，会产生复流形。所以有些函数论问题，仅局限在 n 维复欧几里得空间上考虑是不够的，必须扩产到复流形上讨论。这就是为什么在多复变函数论中，复流形的概念是不可缺少的。关于复流形的研究，紧复流形比一般情形要成熟些。^[1]

作为一维的复流形的黎曼面的研究有着悠久的历史，而一般复流形的研究从20世纪40年代才开始。

现今，它已成为近代数学中十分重要的概念和课题。

考虑R³中的单位球面。它可以被球面分别去掉北极和南极所得到的两个坐标开集所覆盖。用关于北极的球极投影得到一个坐标映射，而关于南极的球极投影后再取共轭复数又得到另一个坐标映射。这样，单位球面也构成一维复流形，称为黎曼球面。

对复射影空间CP^[2]