三代角定理

这个定理用来计算在一个母角角度在360以内的角均分成N份后，得到N个子角，并且在该母角以及每 个子角上做弦，其各个（子角的弦或者弦延长线）与（母角的弦或者延长线）自然相交的角度。这里称这种角为孙角

公式如下：

St =z*(n/2+0.5-t)=m*(n/2+0.5-t)/n

公式中各表示为：

St —— 第几个孙角的角度

z —— 子角的度数

* —— 数学算式中的乘法运算符号

n —— 把母角分成多少等份

/ —— 数学运算符号中的除法运算符号

2 —— 数字2

+ —— 数学运算符号中的加法运算符号

0.5 ——数值0.5

- —— 数学运算符号中的减法运算符号

t ——第几个孙角

m —— 母角的角度

如图所示：

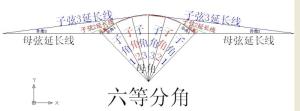把一个母角均分成5等份后，得到5个角度相同的子角（两个子角1、两个子角2、一个子角3，）；在每个子角上做弦（图中红色的线）和母角上做弦（图中绿色的线），并且让各子角弦与母角弦自然相交（如不能相交，做各自的延长线（图中有提示的黑色的线），直至相交为止（子角份数分为奇份数的，中间那条子弦与母弦不能相交，因为它们是处于平行状态！但仍遵守这个定理））；这样这个示例中就产生了4个孙角，它们的各个角度可以用上面的定理，把各变量代进去，就可以把各个孙角的角度给计算出来！

注：（这个示例因为是把母角均分成5份，为奇份数，所以中间那个孙角的角度为0度，所以这个示例只有4个孙角；如果母角的均分份数为偶份数（如6份），那么就有产生6个孙角了！如图：）这个定理可以把360度以内的母角均分成任意份数，计算其子弦与母弦相交产生的各个孙角角度！

发现者：中华人民共和国浙江省丽水市缙云县五云镇洋潭头村（原项山村）：朱雄亮

发现时间：2000年9月12日

发表时间：2011年3月18日