- 三正弦定理

三正弦定理
定理概述
设二面角M-AB-N的度数为![]() ,在平面M上有一条射线AC,它和棱AB所成角为
,在平面M上有一条射线AC,它和棱AB所成角为![]() ,和平面N所成的角为
,和平面N所成的角为![]() ,则
,则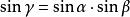 (如图)。
(如图)。
(注明:折叠角公式(又名:三余弦定理)以及三正弦定理的应用为立体几何的解题带来了许多方便。)
若已知二面角其中一个半平面内某直线与二面角的棱所成的角,以及该直线与另一半平面所成的角,则可以求该二面角的正弦值。
定理证明
如上图,过C作CO⊥平面N于点O,过O作直线OB⊥二面角的棱于点B,连OA,CB,则易知△CAO,△CBO,△ABC均为直角三角形.
于是,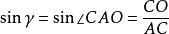 ,
,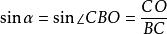 ,
,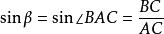 。
。
由此容易推得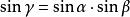 。
。
定理应用
如果将三正弦定理和三余弦定理联合起来,用于解答立体几何综合题,你会发现出乎意料地简单,甚至不用作任何辅助线!
例1 如图,已知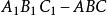 是正三棱柱,D是AC中点,若
是正三棱柱,D是AC中点,若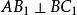 ,求以
,求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角的度数(1994年全国高考理科数学23题)。
为面的二面角的度数(1994年全国高考理科数学23题)。
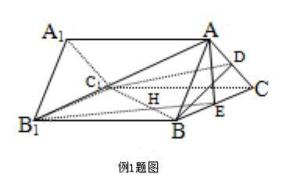 三正弦定理应用之例1题图
三正弦定理应用之例1题图
 三正弦定理应用之例1解答
三正弦定理应用之例1解答
例2 已知Rt△ABC的两直角边AC=2,BC=3.P为斜边AB上一点,现沿CP将此直角三角形折成直二面角A-CP-B(如下图),当AB=![]() 时,求二面角P-AC-B大小(上海市1986年高考试题,难度系数0.28)。
时,求二面角P-AC-B大小(上海市1986年高考试题,难度系数0.28)。
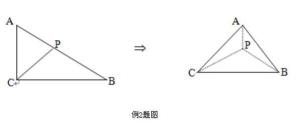 三正弦定理应用之例2题图
三正弦定理应用之例2题图
 三正弦定理应用之例2解答
三正弦定理应用之例2解答
参见
三余弦定理

相关百科


 求购
求购







